Starting with the definition 1 in. = 2.54 cm, find the number of kilometers in 1.00 mile

The density of gold is 19.3 g/cm³. What is this value in kilograms per cubic meter?

According to the label on a bottle of salad dressing, the volume of the contents is 0.473 liter (L). Using only the conversions 1 L = 1000 cm³ and 1 in. = 2.54 cm, express this volume in cubic inches.

How many nanoseconds does it take light to travel 1.00 ft in vacuum? (This result is a useful quantity to remember.)

A certain fuel-efficient hybrid car gets gasoline mileage of 55.0 mpg (miles per gallon). If you are driving this car in Europe and want to compare its mileage with that of other European cars, express this mileage in km/L (L = liter).

The RDA for the trace element selenium is 0.000070 g/day. Express this dose in mg/day.

In the fall of 2002, scientists at Los Alamos National Laboratory determined that the critical mass of neptunium-237 is about 60 kg. The critical mass of a fissionable material is the minimum amount that must be brought together to start a nuclear chain reaction. Neptunium-237 has a density of 19.5 g/cm3. What would be the radius of a sphere of this material that has a critical mass?

Bacteria vary in size, but a diameter of 2.0 μm is not unusual. What are the volume (in cubic centimeters) and surface area (in square millimeters) of a spherical bacterium of that size?

With a wooden ruler, you measure the length of a rectangular piece of sheet metal to be 12 mm. With micrometer calipers, you measure the width of the rectangle to be 5.98 mm. Use the correct number of significant figures: What is the area of the rectangle?

With a wooden ruler, you measure the length of a rectangular piece of sheet metal to be 12 mm. With micrometer calipers, you measure the width of the rectangle to be 5.98 mm. Use the correct number of significant figures: What is the perimeter of the rectangle?

A useful and easy-to-remember approximate value for the number of seconds in a year is π × 107. Determine the percent error in this approximate value. (There are 365.24 days in one year.)

How many gallons of gasoline are used in the United States in one day? Assume that there are two cars for every three people, that each car is driven an average of 10,000 miles per year, and that the average car gets 20 miles per gallon.

Four astronauts are in a spherical space station. If, as is typical, each of them breathes about 500 cm³ of air with each breath, approximately what volume of air (in cubic meters) do these astronauts breathe in a year?

You are using water to dilute small amounts of chemicals in the laboratory, drop by drop. How many drops of water are in a 1.0-L bottle?

How many times does a human heart beat during a person's lifetime? How many gallons of blood does it pump?

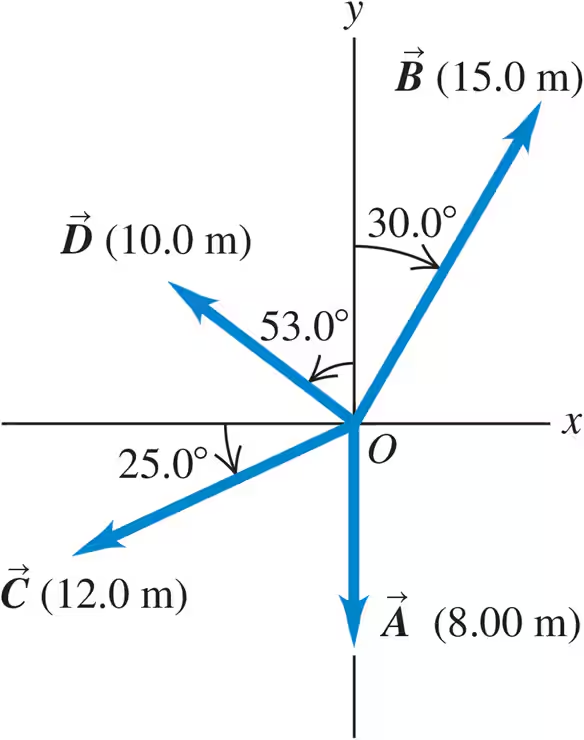
For the vectors A and B in Fig. E1.24, use a scale drawing to find the magnitude and direction of the vector sum A + B

For the vectors A and B in Fig. E1.24, use a scale drawing to find the magnitude and direction of the vector difference A − B.

A spelunker is surveying a cave. She follows a passage 180 m straight west, then 210 m in a direction 45° east of south, and then 280 m at 30° east of north. After a fourth displacement, she finds herself back where she started. Use a scale drawing to determine the magnitude and direction of the fourth displacement.

Let θ be the angle that the vector A makes with the +x-axis, measured counterclockwise from that axis. Find angle θ for a vector that has these components: A_x = 2.00m, A_y = −1.00 m

Compute the x- and y-components of the vectors A, B, C, and D in Fig. E1.24.

Vector A has y-component A_y = +9.60 m. A makes an angle of 32.0° counterclockwise from the +y-axis. (a) What is the x-component of A? (b) What is the magnitude of A?

A postal employee drives a delivery truck over the route shown in Fig. E1.25. Use the method of components to determine the magnitude and direction of her resultant displacement. In a vector-addition diagram (roughly to scale), show that the resultant displacement found from your diagram is in qualitative agreement with the result you obtained by using the method of components.

For the vectors A and B in Fig. E1.24 use the method of components to find the magnitude and direction of the vector sum A + B

For the vectors A and B in Fig. E1.24 use the method of components to find the magnitude and direction of the vector difference A - B

For the vectors A and B in Fig. E1.24 use the method of components to find the magnitude and direction of the vector difference B - A

Find the magnitude and direction of the vector represented by the following pairs of components: A_x = −8.60 cm, A_y = 5.20 cm

A disoriented physics professor drives 3.25 km north, then 2.20 km west, and then 1.50 km south. Find the magnitude and direction of the resultant displacement, using the method of components. In a vector-addition diagram (roughly to scale), show that the resultant displacement found from your diagram is in qualitative agreement with the result you obtained by using the method of components.

Vector A is 2.80 cm long and is 60.0° above the x-axis in the first quadrant. Vector B is 1.90 cm long and is 60.0° below the x-axis in the fourth quadrant (Fig. E1.35). Use components to find the magnitude and direction of A - B In each case, sketch the vector addition or subtraction and show that your numerical answers are in qualitative agreement with your sketch.

In each case, find the x- and y- components of vector A: A = 11.2j - 9.91i

Given two vectors A = 4i + 7j and B = 5i - 2j, find the magnitude of each vector.