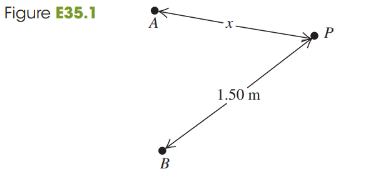
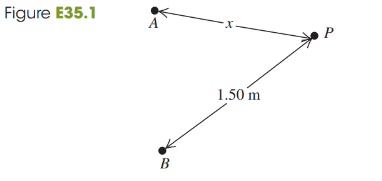
Two small stereo speakers A and B that are 1.40 m apart are sending out sound of wavelength 34 cm in all directions and all in phase. A person at point P starts out equidistant from both speakers and walks so that he is always 1.50 m from speaker B (Fig. E35.1). For what values of x will the sound this person hears be maximally reinforced? Limit your solution to the cases where x ≤ 1.50 m.

Two small stereo speakers A and B that are 1.40 m apart are sending out sound of wavelength 34 cm in all directions and all in phase. A person at point P starts out equidistant from both speakers and walks so that he is always 1.50 m from speaker B (Fig. E35.1). For what values of x will the sound this person hears be cancelled? Limit your solution to the cases where x ≤ 1.50 m.

Two speakers that are 15.0 m apart produce in-phase sound waves of frequency 250.0 Hz in a room where the speed of sound is 340.0 m/s. A woman starts out at the midpoint between the two speakers. The room's walls and ceiling are covered with absorbers to eliminate reflections, and she listens with only one ear for best precision. What does she hear: constructive or destructive interference? Why?

Two speakers that are 15.0 m apart produce in-phase sound waves of frequency 250.0 Hz in a room where the speed of sound is 340.0 m/s. A woman starts out at the midpoint between the two speakers. The room's walls and ceiling are covered with absorbers to eliminate reflections, and she listens with only one ear for best precision. How far from the center must she walk before she first hears the sound maximally enhanced?

Two radio antennas A and B radiate in phase. Antenna B is 120 m to the right of antenna A. Consider point Q along the extension of the line connecting the antennas, a horizontal distance of 40 m to the right of antenna B. The frequency, and hence the wavelength, of the emitted waves can be varied. What is the longest wavelength for which there will be destructive interference at point Q?

Two radio antennas A and B radiate in phase. Antenna B is 120 m to the right of antenna A. Consider point Q along the extension of the line connecting the antennas, a horizontal distance of 40 m to the right of antenna B. The frequency, and hence the wavelength, of the emitted waves can be varied. What is the longest wavelength for which there will be constructive interference at point Q?

Two speakers, emitting identical sound waves of wavelength 2.0 m in phase with each other, and an observer are located as shown in Fig. E35.5. At the observer's location, what is the path difference for waves from the two speakers?

Coherent light with wavelength 450 nm falls on a pair of slits. On a screen 1.80 m away, the distance between dark fringes is 3.90 mm. What is the slit separation?

Two slits spaced 0.450 mm apart are placed 75.0 cm from a screen. What is the distance between the second and third dark lines of the interference pattern on the screen when the slits are illuminated with coherent light with a wavelength of 500 nm?

Coherent light of frequency 6.32 × 10¹⁴ Hz passes through two thin slits and falls on a screen 85.0 cm away. You observe that the third bright fringe occurs at ±3.11 cm on either side of the central bright fringe. (a) How far apart are the two slits? (b) At what distance from the central bright fringe will the third dark fringe occur?

In a two-slit interference pattern, the intensity at the peak of the central maximum is I₀. At a point in the pattern where the phase difference between the waves from the two slits is 60.0°, what is the intensity?

Two slits spaced 0.260 mm apart are 0.900 m from a screen and illuminated by coherent light of wavelength 660 nm. The intensity at the center of the central maximum (u = 0°) is I₀. What is the distance on the screen from the center of the central maximum to the first minimum

Two slits spaced 0.260 mm apart are 0.900 m from a screen and illuminated by coherent light of wavelength 660 nm. The intensity at the center of the central maximum (u = 0°) is I₀. What is the distance on the screen from the center of the central maximum to the point where the intensity has fallen to I₀/2?

What is the thinnest film of a coating with n = 1.42 on glass (n = 1.52) for which destructive interference of the red component (650 nm) of an incident white light beam in air can take place by reflection?

When viewing a piece of art that is behind glass, one often is affected by the light that is reflected off the front of the glass (called glare), which can make it difficult to see the art clearly. One solution is to coat the outer surface of the glass with a film to cancel part of the glare. If the glass has a refractive index of 1.62 and you use TiO₂, which has an index of refraction of 2.62, as the coating, what is the minimum film thickness that will cancel light of wavelength 505 nm?

A uniform film of TiO₂, 1036 nm thick and having index of refraction 2.62, is spread uniformly over the surface of crown glass of refractive index 1.52. Light of wavelength 520.0 nm falls at normal incidence onto the film from air. You want to increase the thickness of this film so that the reflected light cancels. What is the minimum thickness of TiO₂ that you must add so the reflected light cancels as desired?

How far must the mirror M₂ (see Fig. 35.19) of the Michelson interferometer be moved so that 1800 fringes of He-Ne laser light (λ = 633 nm) move across a line in the field of view?

<Image>

Two rectangular pieces of plane glass are laid one upon the other on a table. A thin strip of paper is placed between them at one edge so that a very thin wedge of air is formed. The plates are illuminated at normal incidence by 546-nm light from a mercury-vapor lamp. Interference fringes are formed, with 15.0 fringes per centimeter. Find the angle of the wedge.