Back
BackProblem 1
On a part-time job, you are asked to bring a cylindrical iron rod of length 85.8 cm and diameter 2.85 cm from a storage room to a machinist. Will you need a cart? (To answer, calculate the weight of the rod.)
Problem 2a
A cube 5.0 cm on each side is made of a metal alloy. After you drill a cylindrical hole 2.0 cm in diameter all the way through and perpendicular to one face, you find that the cube weighs 6.30 N. What is the density of this metal?
Problem 4
Gold Brick.You win the lottery and decide to impress your friends by exhibiting a million-dollar cube of gold. At the time, gold is selling for $1282 per troy ounce, and 1.0000 troy ounce equals 31.1035 g. How tall would your million-dollar cube be?
Problem 9
Oceans on Mars. Scientists have found evidence that Mars may once have had an ocean 0.500 km deep. The acceleration due to gravity on Mars is 3.71 m/s2. (a) What would be the gauge pressure at the bottom of such an ocean, assuming it was freshwater? (b) To what depth would you need to go in the earth's ocean to experience the same gauge pressure?
Problem 11
In intravenous feeding, a needle is inserted in a vein in the patient's arm and a tube leads from the needle to a reservoir of fluid (density 1050 kg/m3) located at height h above the arm. The top of the reservoir is open to the air. If the gauge pressure inside the vein is 5980 Pa, what is the minimum value of h that allows fluid to enter the vein? Assume the needle diameter is large enough that you can ignore the viscosity of the liquid.
Problem 12a
A barrel contains a 0.120-m layer of oil floating on water that is 0.250 m deep. The density of the oil is 600 kg/m3. (a) What is the gauge pressure at the oil–water interface? (b) What is the gauge pressure at the bottom of the barrel?
Problem 14a
You are designing a diving bell to withstand the pressure of seawater at a depth of 250 m. (a) What is the gauge pressure at this depth? (You can ignore changes in the density of the water with depth.)
Problem 14b
You are designing a diving bell to withstand the pressure of seawater at a depth of 250 m. What is the gauge pressure at this depth? (You can ignore changes in the density of the water with depth.) At this depth, what is the net force due to the water outside and the air inside the bell on a circular glass window 30.0 cm in diameter if the pressure inside the diving bell equals the pressure at the surface of the water? (Ignore the small variation of pressure over the surface of the window.)
Problem 15a
Ear Damage from Diving. If the force on the tympanic membrane (eardrum) increases by about 1.5 N above the force from atmospheric pressure, the membrane can be damaged. When you go scuba diving in the ocean, below what depth could damage to your eardrum start to occur? The eardrum is typically 8.2 mm in diameter. (Consult Table 12.1.)
Problem 16
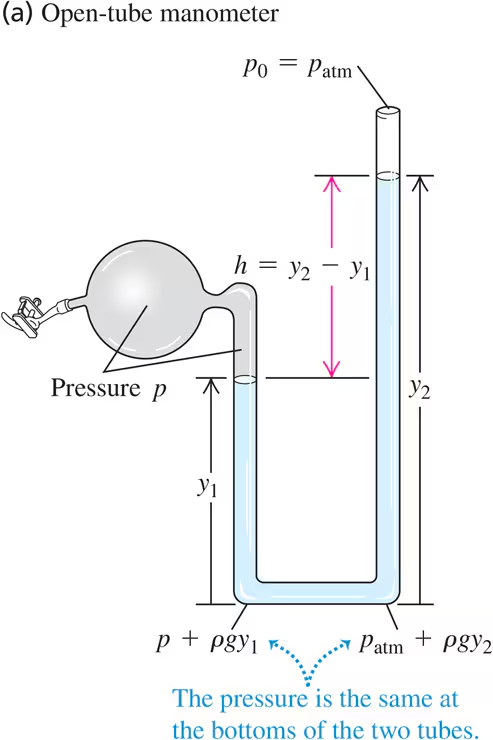
The liquid in the open-tube manometer in Fig. 12.8a is mercury, y1=3.00 cm,and y2=7.00 cm. Atmospheric pressure is 980 millibars. What is (a) the absolute pressure at the bottom of the U-shaped tube; (b) the absolute pressure in the open tube at a depth of 4.00 cm below the free surface; (c) the absolute pressure of the gas in the container; (d) the gauge pressure of the gas in pascals?
Problem 17
BIO. There is a maximum depth at which a diver can breathe through a snorkel tube (Fig. E12.17) because as the depth increases, so does the pressure difference, which tends to collapse the diver's lungs. Since the snorkel connects the air in the lungs to the atmosphere at the surface, the pressure inside the lungs is atmospheric pressure. What is the external– internal pressure difference when the diver's lungs are at a depth of 6.1 m (about 20 ft)? Assume that the diver is in fresh-water. (A scuba diver breathing from compressed air tanks can operate at greater depths than can a snorkeler, since the pressure of the air inside the scuba diver's lungs increases to match the external pressure of the water.)
Problem 18
BIO. The lower end of a long plastic straw is immersed below the surface of the water in a plastic cup. An average person sucking on the upper end of the straw can pull water into the straw to a vertical height of 1.1 m above the surface of the water in the cup. (a) What is the lowest gauge pressure that the average person can achieve inside his lungs? (b) Explain why your answer in part (a) is negative.
Problem 22a
A closed container is partially filled with water. Initially, the air above the water is at atmospheric pressure (1.01×105 Pa) and the gauge pressure at the bottom of the water is 2500 Pa. Then additional air is pumped in, increasing the pressure of the air above the water by 1500 Pa. What is the gauge pressure at the bottom of the water?
Problem 24
Hydraulic Lift II.The piston of a hydraulic automobile lift is 0.30 m in diameter. What gauge pressure, in pascals, is required to lift a car with a mass of 1200 kg? Also express this pressure in atmospheres.
Problem 25b
Exploring Venus. The surface pressure on Venus is 92 atm, and the acceleration due to gravity there is 0.894g. In a future exploratory mission, an upright cylindrical tank of benzene is sealed at the top but still pressurized at 92 atm just above the benzene. The tank has a diameter of 1.72 m, and the benzene column is 11.50 m tall. Ignore any effects due to the very high temperature on Venus. What force does the Venusian atmosphere exert on the outside surface of the bottom of the tank?
Problem 26
A rock has mass 1.80 kg. When the rock is suspended from the lower end of a string and totally immersed in water, the tension in the string is 12.8 N. What is the smallest density of a liquid in which the rock will float?
Problem 27
A 950-kg cylindrical can buoy floats vertically in sea-water. The diameter of the buoy is 0.900 m. Calculate the additional distance the buoy will sink when an 80.0-kg man stands on top of it.
Problem 28
A slab of ice floats on a freshwater lake. What minimum volume must the slab have for a 65.0-kg woman to be able to stand on it without getting her feet wet?
Problem 29
An ore sample weighs 17.50 N in air. When the sample is suspended by a light cord and totally immersed in water, the tension in the cord is 11.20 N. Find the total volume and the density of the sample.
Problem 32ab
A hollow plastic sphere is held below the surface of a freshwater lake by a cord anchored to the bottom of the lake. The sphere has a volume of 0.650 m3 and the tension in the cord is 1120 N. (a) Calculate the buoyant force exerted by the water on the sphere. (b) What is the mass of the sphere?
Problem 32c
A hollow plastic sphere is held below the surface of a freshwater lake by a cord anchored to the bottom of the lake. The sphere has a volume of 0.650 m3 and the tension in the cord is 1120 N. The cord breaks and the sphere rises to the surface. When the sphere comes to rest, what fraction of its volume will be submerged?
Problem 33ab
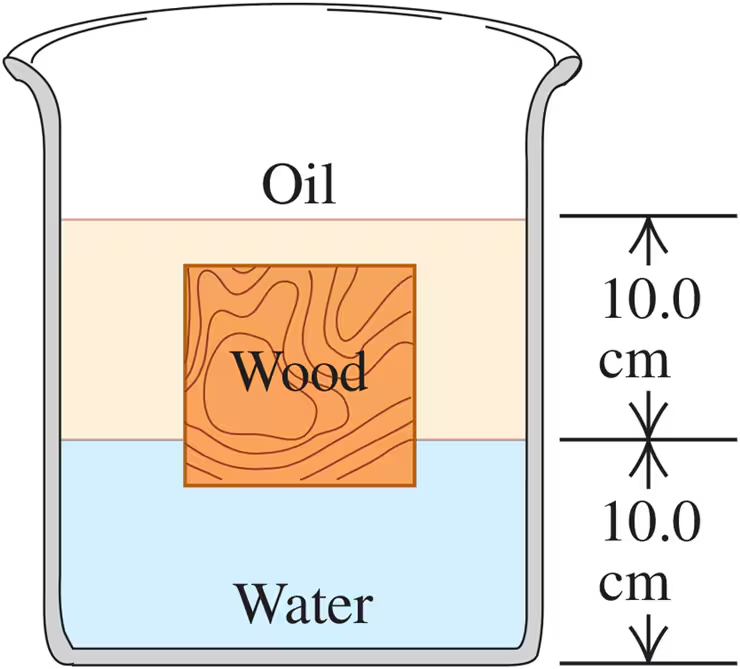
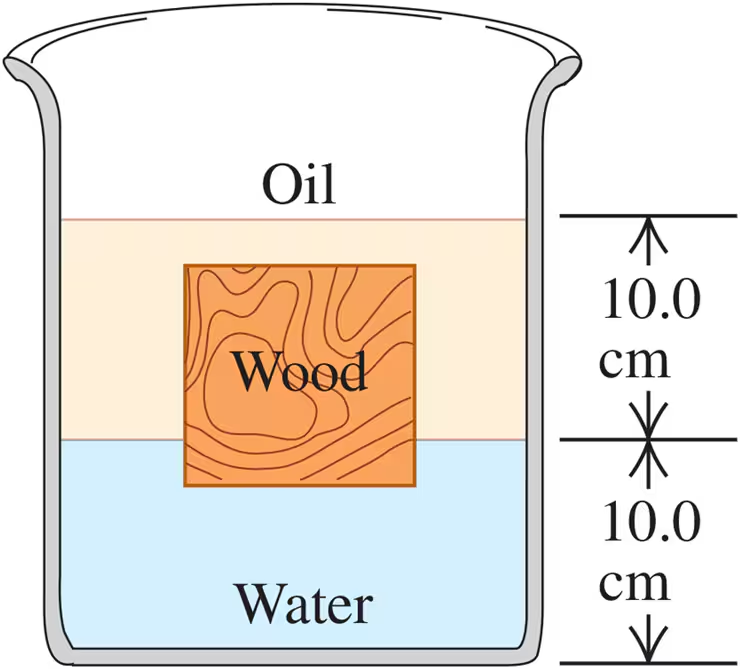
A cubical block of wood, 10.0 cm on a side, floats at the interface between oil and water with its lower surface 1.50 cm below the interface (Fig. E12.33). The density of the oil is 790 kg/m3. (a) What is the gauge pressure at the upper face of the block? (b) What is the gauge pressure at the lower face of the block?
Problem 33c
A cubical block of wood, 10.0 cm on a side, floats at the interface between oil and water with its lower surface 1.50 cm below the interface (Fig. E12.33). The density of the oil is 790 kg/m3. (a) What is the gauge pressure at the upper face of the block? (b) What is the gauge pressure at the lower face of the block?
Problem 37
A shower head has 20 circular openings, each with radius 1.0 mm. The shower head is connected to a pipe with radius 0.80 cm. If the speed of water in the pipe is 3.0 m/s, what is its speed as it exits the shower-head openings?
Problem 38c
Water is flowing in a pipe with a varying cross-sectional area, and at all points the water completely fills the pipe. At point 1 the cross-sectional area of the pipe is 0.070 m2, and the magnitude of the fluid velocity is 3.50 m/s. (c) Calculate the volume of water discharged from the open end of the pipe in 1.00 hour.
Problem 40
Home Repair. You need to extend a 2.50-inch-diameter pipe, but you have only a 1.00-inch-diameter pipe on hand. You make a fitting to connect these pipes end to end. If the water is flowing at 6.00 cm/s in the wide pipe, how fast will it be flowing through the narrow one?
Problem 42
BIO. Artery Blockage. A medical technician is trying to determine what percentage of a patient's artery is blocked by plaque. To do this, she measures the blood pressure just before the region of blockage and finds that it is 1.20×104 Pa, while in the region of blockage it is 1.15×104 Pa. Furthermore, she knows that blood flowing through the normal artery just before the point of blockage is traveling at 30.0 cm/s, and the specific gravity of this patient's blood is 1.06. What percentage of the cross-sectional area of the patient's artery is blocked by the plaque?
Problem 44
A small circular hole 6.00 mm in diameter is cut in the side of a large water tank, 14.0 m below the water level in the tank. The top of the tank is open to the air. Find (a) the speed of efflux of the water and (b) the volume discharged per second.
Problem 46
At one point in a pipeline the water's speed is 3.00 m/s and the gauge pressure is 5.00×104 Pa. Find the gauge pressure at a second point in the line, 11.0 m lower than the first, if the pipe diameter at the second point is twice that at the first.
Problem 48bc
A soft drink (mostly water) flows in a pipe at a beverage plant with a mass flow rate that would fill 220 0.355-L cans per minute. At point 2 in the pipe, the gauge pressure is 152 kPa and the cross-sectional area is 8.00 cm2. At point 1, 1.35 m above point 2, the cross-sectional area is 2.00 cm2. Find the (b) volume flow rate. (c) flow speeds at points 1 and 2.