Calculate the magnitude of the angular momentum of the earth in a circular orbit around the sun. Is it reasonable to model it as a particle? Consult Appendix E and the astronomical data in Appendix F

A hollow, thin-walled sphere of mass $12.0\mathrm{kg}$ and diameter $48.0\text{ cm}$ is rotating about an axle through its center. The angle (in radians) through which it turns as a function of time (in seconds) is given by $\theta \left(t\right)=A{t}^2+B{t}^4$, where A has numerical value $1.50$ and B has numerical value $1.10$. What are the units of the constants A and B?

A small block on a frictionless, horizontal surface has a mass of 0.0250 kg. It is attached to a massless cord passing through a hole in the surface (Fig. E10.40). The block is originally revolving at a distance of 0.300 m from the hole with an angular speed of 2.85 rad/s. The cord is then pulled from below, shortening the radius of the circle in which the block revolves to 0.150 m. Model the block as a particle. Is the angular momentum of the block conserved? Why or why not?

A small block on a frictionless, horizontal surface has a mass of 0.0250 kg. It is attached to a massless cord passing through a hole in the surface (Fig. E10.40). The block is originally revolving at a distance of 0.300 m from the hole with an angular speed of 2.85 rad/s. The cord is then pulled from below, shortening the radius of the circle in which the block revolves to 0.150 m. Model the block as a particle. What is the new angular speed?

A small block on a frictionless, horizontal surface has a mass of 0.0250 kg. It is attached to a massless cord passing through a hole in the surface (Fig. E10.40). The block is originally revolving at a distance of 0.300 m from the hole with an angular speed of 2.85 rad/s. The cord is then pulled from below, shortening the radius of the circle in which the block revolves to 0.150 m. Model the block as a particle. Find the change in kinetic energy of the block.

A small block on a frictionless, horizontal surface has a mass of 0.0250 kg. It is attached to a massless cord passing through a hole in the surface (Fig. E10.40). The block is originally revolving at a distance of 0.300 m from the hole with an angular speed of 2.85 rad/s. The cord is then pulled from below, shortening the radius of the circle in which the block revolves to 0.150 m. Model the block as a particle. How much work was done in pulling the cord?

Under some circumstances, a star can collapse into an extremely dense object made mostly of neutrons and called a neutron star. The density of a neutron star is roughly ${10}^{14}$ times as great as that of ordinary solid matter. Suppose we represent the star as a uniform, solid, rigid sphere, both before and after the collapse. The star's initial radius was $7.0\times {10}^5\text{ km}$ (comparable to our sun); its final radius is 16 km. If the original star rotated once in $30$ days, find the angular speed of the neutron star.

The Spinning Figure Skater. The outstretched hands and arms of a figure skater preparing for a spin can be considered a slender rod pivoting about an axis through its center (Fig. E10.43). When the skater's hands and arms are brought in and wrapped around his body to execute the spin, the hands and arms can be considered a thinwalled, hollow cylinder. His hands and arms have a combined mass of 8.0 kg. When outstretched, they span 1.8 m; when wrapped, they form a cylinder of radius 25 cm. The moment of inertia about the rotation axis of the remainder of his body is constant and equal to 0.40 kg m² . If his original angular speed is 0.40 rev/s, what is his final angular speed?

A solid wood door 1.00 m wide and 2.00 m high is hinged along one side and has a total mass of 40.0 kg. Initially open and at rest, the door is struck at its center by a handful of sticky mud with mass 0.500 kg, traveling perpendicular to the door at 12.0 m/s just before impact. Find the final angular speed of the door. Does the mud make a significant contribution to the moment of inertia?

A large wooden turntable in the shape of a flat uniform disk has a radius of 2.00 m and a total mass of 120 kg. The turntable is initially rotating at 3.00 rad/s about a vertical axis through its center. Suddenly, a 70.0-kg parachutist makes a soft landing on the turntable at a point near the outer edge. Find the angular speed of the turntable after the parachutist lands. (Assume that you can treat the parachutist as a particle.)

A large wooden turntable in the shape of a flat uniform disk has a radius of 2.00 m and a total mass of 120 kg. The turntable is initially rotating at 3.00 rad/s about a vertical axis through its center. Suddenly, a 70.0-kg parachutist makes a soft landing on the turntable at a point near the outer edge. Compute the kinetic energy of the system before and after the parachutist lands. Why are these kinetic energies not equal?

Suppose that an asteroid traveling straight toward the center of the earth were to collide with our planet at the equator and bury itself just below the surface. What would have to be the mass of this asteroid, in terms of the earth's mass M, for the day to become 25.0% longer than it presently is as a result of the collision? Assume that the asteroid is very small compared to the earth and that the earth is uniform throughout.

A small 10.0-g bug stands at one end of a thin uniform bar that is initially at rest on a smooth horizontal table. The other end of the bar pivots about a nail driven into the table and can rotate freely, without friction. The bar has mass 50.0 g and is 100 cm in length. The bug jumps off in the horizontal direction, perpendicular to the bar, with a speed of 20.0 cm/s relative to the table. What is the angular speed of the bar just after the frisky insect leaps?

A thin uniform rod has a length of $0.500\text{ m}$ and is rotating in a circle on a frictionless table. The axis of rotation is perpendicular to the length of the rod at one end and is stationary. The rod has an angular velocity of $0.400\text{ rad/s}$ and a moment of inertia about the axis of $3.00\times {10}^{-3}{\text{kg/m}}^2$. A bug initially standing on the rod at the axis of rotation decides to crawl out to the other end of the rod. When the bug has reached the end of the rod and sits there, its tangential speed is $0.160\text{ m/s}$. The bug can be treated as a point mass. What is the mass of the rod.

A uniform, 4.5-kg, square, solid wooden gate 1.5 m on each side hangs vertically from a frictionless pivot at the center of its upper edge. A 1.1-kg raven flying horizontally at 5.0 m/s flies into this door at its center and bounces back at 2.0 m/s in the opposite direction. What is the angular speed of the gate just after it is struck by the unfortunate raven?

A uniform, 4.5-kg, square, solid wooden gate 1.5 m on each side hangs vertically from a frictionless pivot at the center of its upper edge. A 1.1-kg raven flying horizontally at 5.0 m/s flies into this door at its center and bounces back at 2.0 m/s in the opposite direction. During the collision, why is the angular momentum conserved but not the linear momentum?

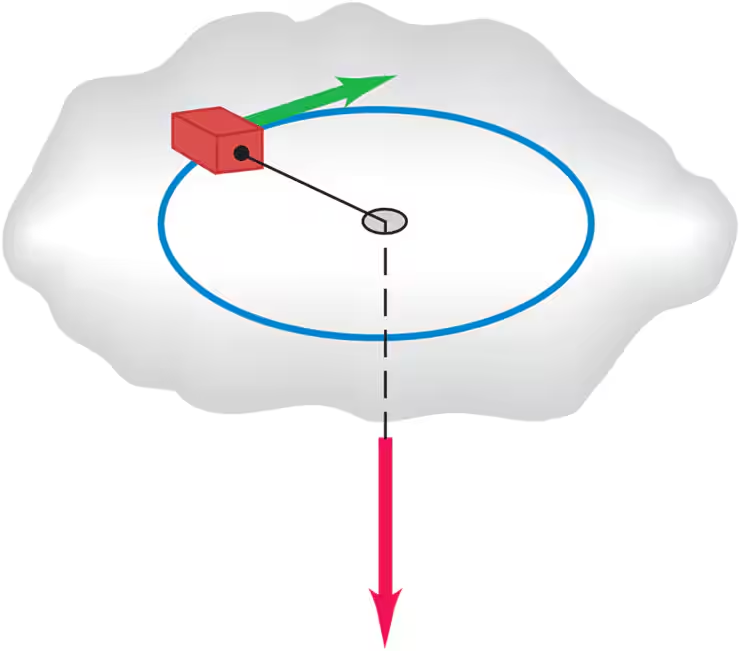
The rotor (flywheel) of a toy gyroscope has mass 0.140 kg. Its moment of inertia about its axis is 1.20 × 10^-4 kg m². The mass of the frame is 0.0250 kg. The gyroscope is supported on a single pivot (Fig. E10.51) with its center of mass a horizontal distance of 4.00 cm from the pivot. The gyroscope is precessing in a horizontal plane at the rate of one revolution in 2.20 s. Find the upward force exerted by the pivot.

<Image>

A certain gyroscope precesses at a rate of 0.50 rad/s when used on earth. If it were taken to a lunar base, where the acceleration due to gravity is 0.165g, what would be its precession rate?