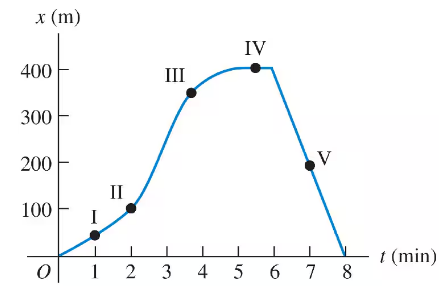
A physics professor leaves her house and walks along the sidewalk toward campus. After $5$ min, it starts to rain, and she returns home. Her distance from her house as a function of time is shown in Fig. E$2.10$. At which of the labeled points is her velocity constant and positive?

A physics professor leaves her house and walks along the sidewalk toward campus. After $5$ min, it starts to rain, and she returns home. Her distance from her house as a function of time is shown in Fig. E$2.10$. At which of the labeled points is her velocity constant and negative?

A physics professor leaves her house and walks along the sidewalk toward campus. After $5$ min, it starts to rain, and she returns home. Her distance from her house as a function of time is shown in Fig. E$2.10$. At which of the labeled points is her velocity decreasing in magnitude?

The table shows test data for the Bugatti Veyron Super Sport, the fastest street car made. The car is moving in a straight line (the $x$-axis).

(a) Sketch a $v_x$-$t$ graph of this car's velocity (in mi/h) as a function of time. Is its acceleration constant?

(b) Calculate the car's average acceleration (in m/s2) between (i) $0$ and $2.1$ s; (ii) $2.1$ s and $20.0$ s; (iii) $20.0$ s and $53$ s. Are these results consistent with your graph in part (a)? (Before you decide to buy this car, it might be helpful to know that only $300$ will be built, it runs out of gas in $12$ minutes at top speed, and it costs more than $\$1.5$ million!)

A race car starts from rest and travels east along a straight and level track. For the first $5.0$ s of the car's motion, the eastward component of the car's velocity is given by $v_x\left(t\right)=$ ($0.860$ m/s³)t². What is the acceleration of the car when $v_x=12.0$ m/s?

A turtle crawls along a straight line, which we will call the $x$-axis with the positive direction to the right. The equation for the turtle's position as a function of time is $x\left(t\right)=50.0$ cm + ($2.00$ cm/s)$$$t$ − ($0.0625$ cm/s²)$t^2$. Find the turtle's initial velocity, initial position, and initial acceleration.

A turtle crawls along a straight line, which we will call the $x$-axis with the positive direction to the right. The equation for the turtle's position as a function of time is $x(t) = 50.0$ cm + ($2.00$ cm/s)$$$t$ − ($0.0625$ cm/s²)$t^2$. At what time $t$ is the velocity of the turtle zero?

A turtle crawls along a straight line, which we will call the $x$-axis with the positive direction to the right. The equation for the turtle's position as a function of time is $x(t) = 50.0$ cm + ($2.00$ cm/s)$$$t$ − ($0.0625$ cm/s²)$t^2$. Sketch graphs of $x$ versus $t$, $v_x$ versus $t$, and $a_x$ versus $t$, for the time interval $t=0$ to $t=40$ s.

An astronaut has left the International Space Station to test a new space scooter. Her partner measures the following velocity changes, each taking place in a $10$-s interval. What are the magnitude, the algebraic sign, and the direction of the average acceleration in each interval? Assume that the positive direction is to the right.

(a) At the beginning of the interval, the astronaut is moving toward the right along the $x$-axis at $15.0$ m/s, and at the end of the interval she is moving toward the right at $5.0$ m/s.

(b) At the beginning she is moving toward the left at $5.0$ m/s, and at the end she is moving toward the left at $15.0$ m/s.

(c) At the beginning she is moving toward the right at $15.0$ m/s, and at the end she is moving toward the left at $15.0$ m/s.

A car's velocity as a function of time is given by$v_x\left(t\right)=\alpha +\beta t^2$, where $\alpha =3.00$ m/s and $\beta =0.100$ m/s³. Calculate the average acceleration for the time interval $t=0$ to $t=5.00$ s.

A car's velocity as a function of time is given by$v_x(t) = α + βt^2$, where $α = 3.00$ m/s and $β = 0.100$ m/s³. Draw $v_x$-$t$ and $a_x$-$t$ graphs for the car's motion between $t=0$ and $t=5.00$ s.

An antelope moving with constant acceleration covers the distance between two points $70.0$ m apart in $6.00$ s. Its speed as it passes the second point is $15.0$ m/s. What is its acceleration?

The fastest measured pitched baseball left the pitcher's hand at a speed of $45.0$ m/s. If the pitcher was in contact with the ball over a distance of $1.50$ m and produced constant acceleration, what acceleration did he give the ball?

In the fastest measured tennis serve, the ball left the racquet at $73.14$ m/s. A served tennis ball is typically in contact with the racquet for $30.0$ ms and starts from rest. Assume constant acceleration. What was the ball's acceleration during this serve?

The human body can survive an acceleration trauma incident (sudden stop) if the magnitude of the acceleration is less than $250$ m/s². If you are in an automobile accident with an initial speed of $105$ km/h ($65$ mi/h) and are stopped by an airbag that inflates from the dashboard, over what distance must the airbag stop you for you to survive the crash?

A pilot who accelerates at more than $4g$ begins to 'gray out' but doesn't completely lose consciousness. Assuming constant acceleration, what is the shortest time that a jet pilot starting from rest can take to reach Mach $4$ (four times the speed of sound) without graying out? (Use $331$ m/s for the speed of sound in cold air.)

A pilot who accelerates at more than $4g$ begins to 'gray out' but doesn't completely lose consciousness. How far would the plane travel during this period of acceleration? (Use $331$ m/s for the speed of sound in cold air.)

A car sits on an entrance ramp to a freeway, waiting for a break in the traffic. Then the driver accelerates with constant acceleration along the ramp and onto the freeway. The car starts from rest, moves in a straight line, and has a speed of $20$ m/s ($45$ mi/h) when it reaches the end of the $120$-m-long ramp. What is the acceleration of the car?

A car sits on an entrance ramp to a freeway, waiting for a break in the traffic. Then the driver accelerates with constant acceleration along the ramp and onto the freeway. The car starts from rest, moves in a straight line, and has a speed of $20$ m/s ($45$ mi/h) when it reaches the end of the $120$-m-long ramp. How much time does it take the car to travel the length of the ramp?

At launch a rocket ship weighs $4.5$ million pounds. When it is launched from rest, it takes $8.00$ s to reach $161$ km/h; at the end of the first $1.00$ min, its speed is $1610$ km/h. What is the average acceleration (in m/s²) of the rocket (i) during the first $8.00$ s and (ii) between $8.00$ s and the end of the first $1.00$ min?

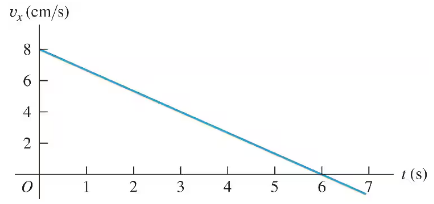
A cat walks in a straight line, which we shall call the $x$-axis, with the positive direction to the right. As an observant physicist, you make measurements of this cat's motion and construct a graph of the feline's velocity as a function of time (Fig. E$2.30$). Find the cat's velocity at $t=4.0$ s and at $t=7.0$ s.

A cat walks in a straight line, which we shall call the $x$-axis, with the positive direction to the right. As an observant physicist, you make measurements of this cat's motion and construct a graph of the feline's velocity as a function of time (Fig. E$2.30$). What is the cat's acceleration at $t=3.0$ s? At $t=6.0$ s? At $t=7.0$ s?

A cat walks in a straight line, which we shall call the $x$-axis, with the positive direction to the right. As an observant physicist, you make measurements of this cat's motion and construct a graph of the feline's velocity as a function of time (Fig. E$2.30$). What distance does the cat move during the first $4.5$ s? From $t=0$ to $t=7.5$ s?

A cat walks in a straight line, which we shall call the $x$-axis, with the positive direction to the right. As an observant physicist, you make measurements of this cat's motion and construct a graph of the feline's velocity as a function of time (Fig. E$2.30$). Assuming that the cat started at the origin, sketch clear graphs of the cat's acceleration and position as functions of time.

A small block has constant acceleration as it slides down a frictionless incline. The block is released from rest at the top of the incline, and its speed after it has traveled $6.80$ m to the bottom of the incline is $3.80$ m/s. What is the speed of the block when it is $3.40$ m from the top of the incline?

At the instant the traffic light turns green, a car that has been waiting at an intersection starts ahead with a constant acceleration of $2.80$ m/s². At the same instant a truck, traveling with a constant speed of $20.0$ m/s, overtakes and passes the car. How far beyond its starting point does the car overtake the truck?

At the instant the traffic light turns green, a car that has been waiting at an intersection starts ahead with a constant acceleration of $2.80$ m/s². At the same instant a truck, traveling with a constant speed of $20.0$ m/s, overtakes and passes the car. How fast is the car traveling when it overtakes the truck?

If a flea can jump straight up to a height of $0.440$ m, what is its initial speed as it leaves the ground?

If a flea can jump straight up to a height of $0.440$ m, How long is it in the air?

A small rock is thrown vertically upward with a speed of $22.0$ m/s from the edge of the roof of a $30.0$-m-tall building. The rock doesn't hit the building on its way back down and lands on the street below. Ignore air resistance. What is the speed of the rock just before it hits the street?