Back
BackProblem 2a
In an experiment, a shearwater (a seabird) was taken from its nest, flown km away, and released. The bird found its way back to its nest days after release. If we place the origin at the nest and extend the –axis to the release point, what was the bird's average velocity in m/s for the return flight?
Problem 3
You normally drive on the freeway between San Diego and Los Angeles at an average speed of km/h ( mi/h), and the trip takes h and min. On a Friday afternoon, however, heavy traffic slows you down and you drive the same distance at an average speed of only km/h ( mi/h). How much longer does the trip take?
Problem 5
Starting from the front door of a ranch house, you walk m due east to a windmill, turn around, and then slowly walk m west to a bench, where you sit and watch the sunrise. It takes you s to walk from the house to the windmill and then s to walk from the windmill to the bench. For the entire trip from the front door to the bench, what are your (a) average velocity? (b) average speed?
Problem 7a
A car is stopped at a traffic light. It then travels along a straight road such that its distance from the light is given by , where m/s2 and m/s3. Calculate the average velocity of the car for the time interval to s.
Problem 7b
A car is stopped at a traffic light. It then travels along a straight road such that its distance from the light is given by , where m/s2 and m/s3. Calculate the instantaneous velocity of the car at , s, and s.
Problem 9a
A ball moves in a straight line (the -axis). The graph in Fig. E shows this ball's velocity as a function of time. What are the ball's average speed and average velocity during the first s?

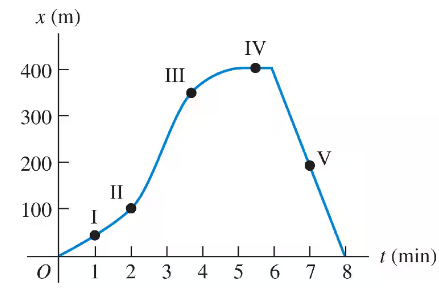
Problem 10a
A physics professor leaves her house and walks along the sidewalk toward campus. After min, it starts to rain, and she returns home. Her distance from her house as a function of time is shown in Fig. E. At which of the labeled points is her velocity zero?
Problem 10b
A physics professor leaves her house and walks along the sidewalk toward campus. After min, it starts to rain, and she returns home. Her distance from her house as a function of time is shown in Fig. E. At which of the labeled points is her velocity constant and positive?
Problem 10c
A physics professor leaves her house and walks along the sidewalk toward campus. After min, it starts to rain, and she returns home. Her distance from her house as a function of time is shown in Fig. E. At which of the labeled points is her velocity constant and negative?
Problem 10e
A physics professor leaves her house and walks along the sidewalk toward campus. After min, it starts to rain, and she returns home. Her distance from her house as a function of time is shown in Fig. E. At which of the labeled points is her velocity decreasing in magnitude?
Problem 13
The table shows test data for the Bugatti Veyron Super Sport, the fastest street car made. The car is moving in a straight line (the -axis).
(a) Sketch a - graph of this car's velocity (in mi/h) as a function of time. Is its acceleration constant?
(b) Calculate the car's average acceleration (in m/s2) between (i) and s; (ii) s and s; (iii) s and s. Are these results consistent with your graph in part (a)? (Before you decide to buy this car, it might be helpful to know that only will be built, it runs out of gas in minutes at top speed, and it costs more than million!)
Problem 14
A race car starts from rest and travels east along a straight and level track. For the first s of the car's motion, the eastward component of the car's velocity is given by ( m/s3)t2. What is the acceleration of the car when m/s?
Problem 15a
A turtle crawls along a straight line, which we will call the -axis with the positive direction to the right. The equation for the turtle's position as a function of time is cm + ( cm/s) − ( cm/s2). Find the turtle's initial velocity, initial position, and initial acceleration.
Problem 15b
A turtle crawls along a straight line, which we will call the -axis with the positive direction to the right. The equation for the turtle's position as a function of time is cm + ( cm/s) − ( cm/s2). At what time is the velocity of the turtle zero?
Problem 15e
A turtle crawls along a straight line, which we will call the -axis with the positive direction to the right. The equation for the turtle's position as a function of time is cm + ( cm/s) − ( cm/s2). Sketch graphs of versus , versus , and versus , for the time interval to s.
Problem 16
An astronaut has left the International Space Station to test a new space scooter. Her partner measures the following velocity changes, each taking place in a -s interval. What are the magnitude, the algebraic sign, and the direction of the average acceleration in each interval? Assume that the positive direction is to the right.
(a) At the beginning of the interval, the astronaut is moving toward the right along the -axis at m/s, and at the end of the interval she is moving toward the right at m/s.
(b) At the beginning she is moving toward the left at m/s, and at the end she is moving toward the left at m/s.
(c) At the beginning she is moving toward the right at m/s, and at the end she is moving toward the left at m/s.
Problem 17a
A car's velocity as a function of time is given by, where m/s and m/s3. Calculate the average acceleration for the time interval to s.
Problem 17c
A car's velocity as a function of time is given by, where m/s and m/s3. Draw - and - graphs for the car's motion between and s.
Problem 19b
An antelope moving with constant acceleration covers the distance between two points m apart in s. Its speed as it passes the second point is m/s. What is its acceleration?
Problem 21a
The fastest measured pitched baseball left the pitcher's hand at a speed of m/s. If the pitcher was in contact with the ball over a distance of m and produced constant acceleration, what acceleration did he give the ball?
Problem 22a
In the fastest measured tennis serve, the ball left the racquet at m/s. A served tennis ball is typically in contact with the racquet for ms and starts from rest. Assume constant acceleration. What was the ball's acceleration during this serve?
Problem 23
The human body can survive an acceleration trauma incident (sudden stop) if the magnitude of the acceleration is less than m/s2. If you are in an automobile accident with an initial speed of km/h ( mi/h) and are stopped by an airbag that inflates from the dashboard, over what distance must the airbag stop you for you to survive the crash?
Problem 24a
A pilot who accelerates at more than begins to 'gray out' but doesn't completely lose consciousness. Assuming constant acceleration, what is the shortest time that a jet pilot starting from rest can take to reach Mach (four times the speed of sound) without graying out? (Use m/s for the speed of sound in cold air.)
Problem 24b
A pilot who accelerates at more than begins to 'gray out' but doesn't completely lose consciousness. How far would the plane travel during this period of acceleration? (Use m/s for the speed of sound in cold air.)
Problem 28a
A car sits on an entrance ramp to a freeway, waiting for a break in the traffic. Then the driver accelerates with constant acceleration along the ramp and onto the freeway. The car starts from rest, moves in a straight line, and has a speed of m/s ( mi/h) when it reaches the end of the -m-long ramp. What is the acceleration of the car?
Problem 28b
A car sits on an entrance ramp to a freeway, waiting for a break in the traffic. Then the driver accelerates with constant acceleration along the ramp and onto the freeway. The car starts from rest, moves in a straight line, and has a speed of m/s ( mi/h) when it reaches the end of the -m-long ramp. How much time does it take the car to travel the length of the ramp?
Problem 29a
At launch a rocket ship weighs million pounds. When it is launched from rest, it takes s to reach km/h; at the end of the first min, its speed is km/h. What is the average acceleration (in m/s2) of the rocket (i) during the first s and (ii) between s and the end of the first min?
Problem 30a
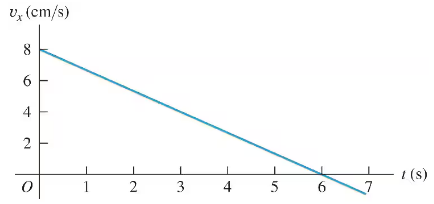
A cat walks in a straight line, which we shall call the -axis, with the positive direction to the right. As an observant physicist, you make measurements of this cat's motion and construct a graph of the feline's velocity as a function of time (Fig. E). Find the cat's velocity at s and at s.
Problem 30b
A cat walks in a straight line, which we shall call the -axis, with the positive direction to the right. As an observant physicist, you make measurements of this cat's motion and construct a graph of the feline's velocity as a function of time (Fig. E). What is the cat's acceleration at s? At s? At s?
Problem 30c
A cat walks in a straight line, which we shall call the -axis, with the positive direction to the right. As an observant physicist, you make measurements of this cat's motion and construct a graph of the feline's velocity as a function of time (Fig. E). What distance does the cat move during the first s? From to s?