A horizontal meter stick is centered at the bottom of a 3.0-m-deep, 3.0-m-wide pool of water. Suppose you place your eye just above the edge of the pool and look along the direction of the meter stick. What angle do you observe between the two ends of the meter stick if the pool is (a) empty and (b) completely filled with water?

A 4.0-m-wide swimming pool is filled to the top. The bottom of the pool becomes completely shaded in the afternoon when the sun is 20° above the horizon. How deep is the pool?

An astronaut is exploring an unknown planet when she accidentally drops an oxygen canister into a 1.50-m-deep pool filled with an unknown liquid. Although she dropped the canister 21 cm from the edge, it appears to be 31 cm away when she peers in from the edge. What is the liquid's index of refraction? Assume that the planet's atmosphere is similar to earth's.

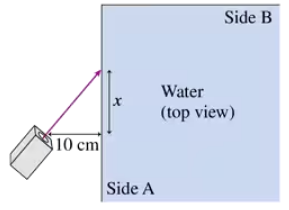
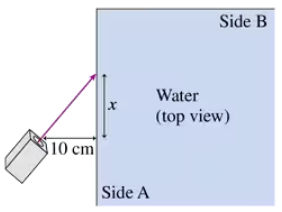
Shown from above in FIGURE P34.54 is one corner of a rectangular box filled with water. A laser beam starts 10 cm from side A of the container and enters the water at position x. You can ignore the thin walls of the container. If x = 15 cm, does the laser beam refract back into the air through side B or reflect from side B back into the water? Determine the angle of refraction or reflection.

Shown from above in FIGURE P34.54 is one corner of a rectangular box filled with water. A laser beam starts 10 cm from side A of the container and enters the water at position x. You can ignore the thin walls of the container. Find the minimum value of x for which the laser beam passes through side B and emerges into the air.

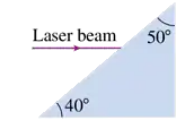
A horizontal laser beam enters the glass prism shown in FIGURE P34.55. When the laser beam exits the prism, by what angle will it have been deflected from horizontal?

Optical engineers need to know the cone of acceptance of an optical fiber. This is the maximum angle that an entering light ray can make with the axis of the fiber if it is to be guided down the fiber. What is the cone of acceptance of an optical fiber for which the index of refraction of the core is 1.55 while that of the cladding is 1.45? You can model the fiber as a cylinder with a flat entrance face.

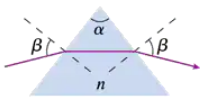
There's one angle of incidence β onto a prism for which the light inside an isosceles prism travels parallel to the base and emerges at angle β. A laboratory measurement finds that β=52.2° for a prism shaped like an equilateral triangle. What is the prism's index of refraction?

You're visiting the shark tank at the aquarium when you see a 2.5-m-long shark that appears to be swimming straight toward you at 2.0 m/s. What is the shark's actual speed through the water? You can ignore the glass wall of the tank.

Paraxial light rays approach a transparent sphere parallel to an optical axis passing through the center of the sphere. The rays come to a focus on the far surface of the sphere. What is the sphere's index of refraction?

BIO A dentist uses a curved mirror to view the back side of teeth in the upper jaw. Suppose she wants an upright image with a magnification of 1.5 when the mirror is 1.2 cm from a tooth. Should she use a convex or a concave mirror? What focal length should it have?

BIO A keratometer is an optical device used to measure the radius of curvature of the eye's cornea—its entrance surface. This measurement is especially important when fitting contact lenses, which must match the cornea's curvature. Most light incident on the eye is transmitted into the eye, but some light reflects from the cornea, which, due to its curvature, acts like a convex mirror. The keratometer places a small, illuminated ring of known diameter 7.5 cm in front of the eye. The optometrist, using an eyepiece, looks through the center of this ring and sees a small virtual image of the ring that appears to be behind the cornea. The optometrist uses a scale inside the eyepiece to measure the diameter of the image and calculate its magnification. Suppose the optometrist finds that the magnification for one patient is 0.049. What is the absolute value of the radius of curvature of her cornea?

A 2.0-cm-tall candle flame is 2.0 m from a wall. You happen to have a lens with a focal length of 32 cm. How many places can you put the lens to form a well-focused image of the candle flame on the wall? For each location, what are the height and orientation of the image?

A 25-cm-long rod lies along the optical axis of a converging lens, perpendicular to the lens plane. The lens has a 30 cm focal length. The rod's real , along the optical axis on the other side of the lens, is also 25 cm long. What is the distance from the lens to the nearest end of the rod?

An old-fashioned slide projector needs to create a 98-cm-high of a 2.0-cm-tall slide. The screen is 300 cm from the slide. What focal length does the lens need? Assume that it is a thin lens.

A lightbulb is 3.0 m from a wall. What are the focal length and the position (measured from the bulb) of a lens that will form an on the wall that is twice the size of the lightbulb?

CALC A converging lens with focal length f creates a real image of an object. What is the minimum possible distance between the object and its image? Your answer will be a multiple of f.

A plano-concave glass lens (flat on one side, concave on the other) creates an with magnification +0.40 of an object 75 cm from the lens. What is the radius of curvature of the lens's curved surface?

An object is 60 cm from a screen. What are the radii of a symmetric converging plastic lens (i.e., two equally curved surfaces) that will form an image on the screen twice the height of the object?

CALC A wildlife photographer with a 200-mm-focal-length telephoto lens on his camera is taking a picture of a rhinoceros that is 100 m away. Suddenly, the rhino starts charging straight toward the photographer at a speed of 5.0 m/s. What is the speed, in μm/s, image of the of the rhinoceros? Is the image moving toward or away from the lens?

Some electro-optic materials can change their index of refraction in response to an applied voltage. Suppose a plano-convex lens (flat on one side, a 15.0 cm radius of curvature on the other), made from a material whose normal index of refraction is 1.500, is creating an image of an object that is 50.0 cm from the lens. By how much would the index of refraction need to be increased to move the image 5.0 cm closer to the lens?

A 2.0-cm-tall object is placed in front of a mirror. A 1.0-cm-tall upright image is formed behind the mirror, 150 cm from the object. What is the focal length of the mirror?

The mirror in FIGURE CP34.79 is covered with a piece of glass whose thickness at the center equals the mirror's radius of curvature. A point source of light is outside the glass. How far from the mirror is the image of this source?

Consider a lens having index of refraction n₂ and surfaces with radii R₁ and R₂. The lens is immersed in a fluid that has index of refraction n₁. A symmetric converging glass lens (i.e., two equally curved surfaces) has two surfaces with radii of 40 cm. Find the focal length of this lens in air and the focal length of this lens in water.

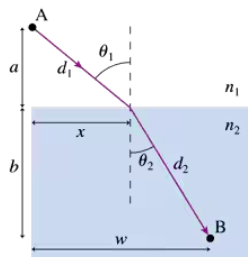
CALC FIGURE CP34.81 shows a light ray that travels from point A to point B. The ray crosses the boundary at position x, making angles θ₁ and θ₂ in the two media. Suppose that you did not know Snell's law. You've proven that Snell's law is equivalent to the statement that 'light traveling between two points follows the path that requires the shortest time.' This interesting way of thinking about refraction is called Fermat's principle. Write an expression for the time t it takes the light ray to travel from A to B. Your expression should be in terms of the distances a, b, and w; the variable x; and the indices of refraction n₁ and n₂.

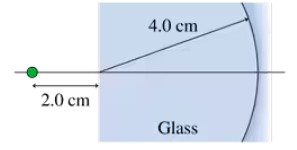
A fortune teller's 'crystal ball' (actually just glass) is 10 cm in diameter. Her secret ring is placed 6.0 cm from the edge of the ball. An image of the ring appears on the opposite side of the crystal ball. How far is the image from the center of the ball?

A fortune teller's 'crystal ball' (actually just glass) is 10 cm in diameter. Her secret ring is placed 6.0 cm from the edge of the ball. The crystal ball is removed and a thin lens is placed where the center of the ball had been. If the image is still in the same position, what is the focal length of the lens?