A double-slit experiment is set up using a helium-neon laser (λ = 633 nm). Then a very thin piece of glass (n = 1.50) is placed over one of the slits. Afterward, the central point on the screen is occupied by what had been the m = 10 dark fringe. How thick is the glass?

FIGURE CP33.73 shows two nearly overlapped intensity peaks of the sort you might produce with a diffraction grating (see Figure 33.9b). As a practical matter, two peaks can just barely be resolved if their spacing Δy equals the width w of each peak, where w is measured at half of the peak’s height. Two peaks closer together than w will merge into a single peak. We can use this idea to understand the resolution of a diffraction grating. In the small-angle approximation, the position of the m = 1 peak of a diffraction grating falls at the same location as the m = 1 fringe of a double slit: y₁ = λL/d. Suppose two wavelengths differing by Δλ pass through a grating at the same time. Find an expression for Δy, the separation of their first-order peaks.

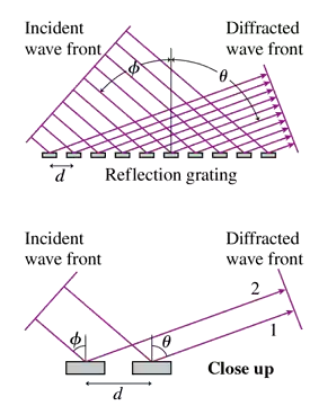
FIGURE CP33.74 shows light of wavelength λ incident at angle ϕ on a reflection grating of spacing d. We want to find the angles θ_m at which constructive interference occurs. Light of wavelength 500 nm is incident at ϕ=40° on a reflection grating having 700 reflection lines/mm. Find all angles θ_m at which light is diffracted. Negative values of θ_m are interpreted as an angle left of the vertical.