Back
BackProblem 1
The earth’s magnetic field strength is 5.0×10−5 T. How fast would you have to drive your car to create a 1.0 V motional emf along your 1.0-m-tall radio antenna? Assume that the motion of the antenna is perpendicular to .
Problem 2a
INT A 10-cm-long wire is pulled along a U-shaped conducting rail in a perpendicular magnetic field. The total resistance of the wire and rail is 0.20 Ω. Pulling the wire at a steady speed of 4.0 m/s causes 4.0 W of power to be dissipated in the circuit. How big is the pulling force?
Problem 3
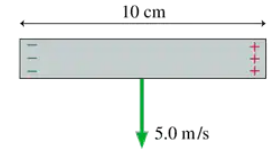
A potential difference of 0.050 V is developed across the 10-cm-long wire of FIGURE EX30.3 as it moves through a magnetic field perpendicular to the figure. What are the strength and direction (in or out) of the magnetic field?
Problem 5
What is the magnitude of the magnetic flux through the loop shown in FIGURE EX30.5?
Problem 6
An equilateral triangle 8.0 cm on a side is in a 5.0 mT uniform magnetic field. The magnetic flux through the triangle is 6.0 μWb. What is the angle between the magnetic field and an axis perpendicular to the plane of the triangle?
Problem 8
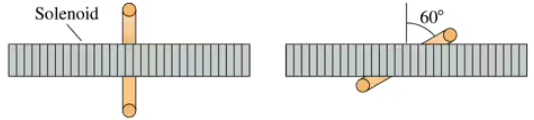
FIGURE EX30.8 shows a 2.0-cm-diameter solenoid passing through the center of a 6.0-cm-diameter loop. The magnetic field inside the solenoid is 0.20 T. What is the magnitude of the magnetic flux through the loop when it is perpendicular to the solenoid and when it is tilted at a 60° angle?
Problem 9b
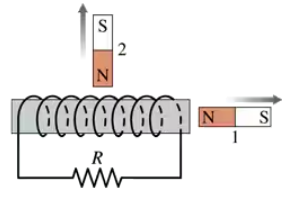
A solenoid is wound as shown in FIGURE EX30.9. Is there an induced current as magnet 2 is moved away from the solenoid? If so, what is the current direction through resistor R?
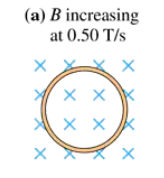
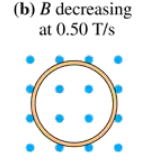
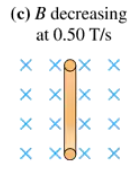
Problem 13
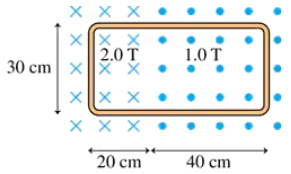
FIGURE EX30.13 shows a 10-cm-diameter loop in three different magnetic fields. The loop's resistance is 0.20 Ω. For each, what are the size and direction of the induced current?
Problem 16
A 1000-turn coil of wire 1.0 cm in diameter is in a magnetic field that increases from 0.10 T to 0.30 T in 10 ms. The axis of the coil is parallel to the field. What is the emf of the coil?
Problem 17a
CALC A 5.0-cm-diameter coil has 20 turns and a resistance of 0.50 Ω. A magnetic field perpendicular to the coil is B = 0.020t + 0.010t2, where B is in tesla and t is in seconds. Find an expression for the induced current I(t) as a function of time.
Problem 17b
CALC A 5.0-cm-diameter coil has 20 turns and a resistance of 0.50 Ω. A magnetic field perpendicular to the coil is B = 0.020t + 0.010t2, where B is in tesla and t is in seconds. Evaluate I at t = 5 s and t = 10 s.
Problem 19
FIGURE EX30.19 shows the current as a function of time through a 20-cm-long, 4.0-cm-diameter solenoid with 400 turns. Draw a graph of the induced electric field strength as a function of time at a point 1.0 cm from the axis of the solenoid.
Problem 20
The magnetic field inside a 5.0-cm-diameter solenoid is 2.0 T and decreasing at 4.0 T/s. What is the electric field strength inside the solenoid at a point (a) on the axis and (b) 2.0 cm from the axis?
Problem 21
A 12-cm-diameter, 1.0-m-long solenoid is wound with 2000 turns of superconducting wire. When the magnet is turned on, the current increases from 0 to Imax in 2.5 s. At t = 1.0 s, the induced electric field midway between the axis and the windings is 7.5×10−3 V/m. What is the solenoid's steady magnetic field strength?
Problem 22a
Electricity is distributed from electrical substations to neighborhoods at 15,000 V. This is a 60 Hz oscillating (AC) voltage. Neighborhood transformers, seen on utility poles, step this voltage down to the 120 V that is delivered to your house. a. How many turns does the primary coil on the transformer have if the secondary coil has 100 turns?
Problem 22b
Electricity is distributed from electrical substations to neighborhoods at 15,000 V. This is a 60 Hz oscillating (AC) voltage. Neighborhood transformers, seen on utility poles, step this voltage down to the 120 V that is delivered to your house. No energy is lost in an ideal transformer, so the output power Pout from the secondary coil equals the input power Pin to the primary coil. Suppose a neighborhood transformer delivers 250 A at 120 V. What is the current in the 15,000 V line from the substation?
Problem 24
What is the potential difference across a 10 mH inductor if the current through the inductor drops from 150 mA to 50 mA in 10 μs? What is the direction of this potential difference? That is, does the potential increase or decrease along the direction of the current?
Problem 26
How much energy is stored in a 3.0-cm-diameter, 12-cm-long solenoid that has 200 turns of wire and carries a current of 0.80 A?
Problem 28a
BIO MRI (magnetic resonance imaging) is a medical technique that produces detailed 'pictures' of the interior of the body. The patient is placed into a solenoid that is 40 cm in diameter and 1.0 m long. A 100 A current creates a 5.0 T magnetic field inside the solenoid. To carry such a large current, the solenoid wires are cooled with liquid helium until they become superconducting (no electric resistance). How much magnetic energy is stored in the solenoid? Assume that the magnetic field is uniform within the solenoid and quickly drops to zero outside the solenoid.
Problem 29
A 2.0 mH inductor is connected in parallel with a variable capacitor. The capacitor can be varied from 100 pF to 200 pF. What is the range of oscillation frequencies for this circuit?
Problem 31
BIO An MRI machine needs to detect signals that oscillate at very high frequencies. It does so with an LC circuit containing a 15 mH coil. To what value should the capacitance be set to detect a 450 MHz signal?
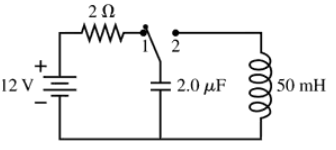
Problem 32b
The switch in FIGURE EX30.32 has been in position 1 for a long time. It is changed to position 2 at t = 0 s. What is the first time at which the current is maximum?
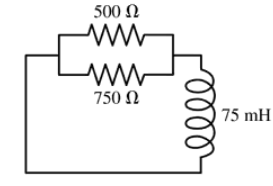
Problem 35
At t = 0 s, the current in the circuit in FIGURE EX30.35 is I0. At what time in μs is the current (1/2)I0?
Problem 38
A 100-turn, 2.0-cm-diameter coil is at rest with its axis vertical. A uniform magnetic field 60° away from vertical increases from 0.50 T to 1.50 T in 0.60 s. What is the induced emf in the coil?
Problem 40
CALC A 10 cm×10 cm square loop of wire lies in the xy-plane. The magnetic field in this region of space is , where t is in s. What is the emf induced in the loop at (a) t = 0.5 s and (b) t = 1.0 s?
Problem 43b
CALC An 8.0 cm×8.0 cm square loop is halfway into a magnetic field perpendicular to the plane of the loop. The loop's mass is 10 g and its resistance is 0.010 Ω. A switch is closed at t = 0 s, causing the magnetic field to increase from 0 to 1.0 T in 0.010 s. Hint: What is the impulse on the loop? With what speed is the loop 'kicked' away from the magnetic field?
Problem 45
A 2.0 cm×2.0 cm square loop of wire with resistance 0.010 Ω has one edge parallel to a long straight wire. The near edge of the loop is 1.0 cm from the wire. The current in the wire is increasing at the rate of 100 A/s. What is the current in the loop?
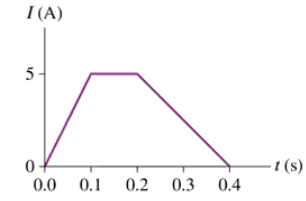
Problem 47
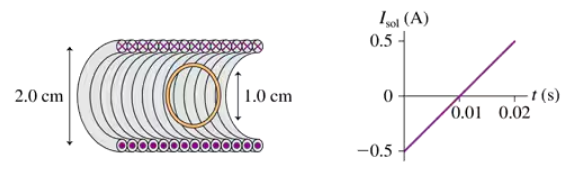
FIGURE P30.47 shows a 1.0-cm-diameter loop with R = 0.50 Ω inside a 2.0-cm-diameter solenoid. The solenoid is 8.0 cm long, has 120 turns, and carries the current shown in the graph. A positive current is cw when seen from the left. Determine the current in the loop at t = 0.010 s.
Problem 48
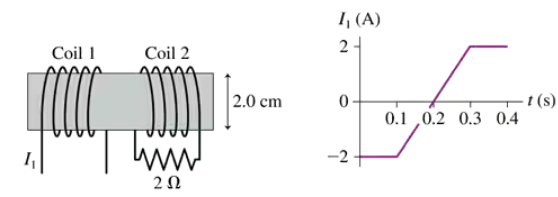
FIGURE P30.48 shows two 20-turn coils tightly wrapped on the same 2.0-cm-diameter cylinder with 1.0-mm-diameter wire. The current through coil 1 is shown in the graph. Determine the current in coil 2 at (a) t = 0.05 s and (b) t = 0.25 s. A positive current is into the figure at the top of a loop. Assume that the magnetic field of coil 1 passes entirely through coil 2.
Problem 49
CALC An electric generator has an 18-cm-diameter, 120-turn coil that rotates at 60 Hz in a uniform magnetic field that is perpendicular to the rotation axis. What magnetic field strength is needed to generate a peak voltage of 170 V?