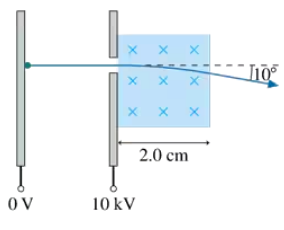
An electron in a cathode-ray tube is accelerated through a potential difference of 10 kV, then passes through the 2.0-cm-wide region of uniform magnetic field in FIGURE P29.60. What field strength will deflect the electron by 10°?

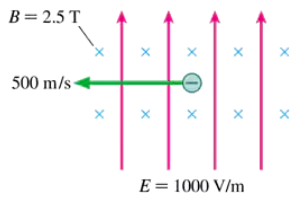
An antiproton (same properties as a proton except that q = -e) is moving in the combined electric and magnetic fields of FIGURE P29.61. What are the magnitude and direction of the antiproton's acceleration at this instant?

A 65-cm-diameter cyclotron uses a 500 V oscillating potential difference between the dees. What is the maximum kinetic energy of a proton if the magnetic field strength is 0.75 T?

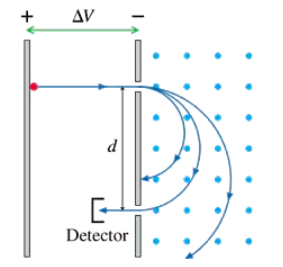
FIGURE P29.64 shows a mass spectrometer, an analytical instrument used to identify the various molecules in a sample by measuring their charge-to-mass ratio q/m. The sample is ionized, the positive ions are accelerated (starting from rest) through a potential difference ∆V, and they then enter a region of uniform magnetic field. The field bends the ions into circular trajectories, but after just half a circle they either strike the wall or pass through a small opening to a detector. As the accelerating voltage is slowly increased, different ions reach the detector and are measured. Consider a mass spectrometer with a 200.00 mT magnetic field and an 8.0000 cm spacing between the entrance and exit holes. To five significant figures, what accelerating potential differences ∆V are required to detect the ions (a) O₂⁺ (b) N₂⁺ and (c) CO⁺? See Exercise 29 for atomic masses; the mass of the missing electron is less than 0.001 u and is not relevant at this level of precision. Although N₂⁺ and CO⁺ both have a nominal molecular mass of 28, they are easily distinguished by virtue of their slightly different accelerating voltages. Use the following constants: 1 u = 1.6605 x 10⁻²⁷ kg, e = 1.6022 x 10⁻¹⁹ C.

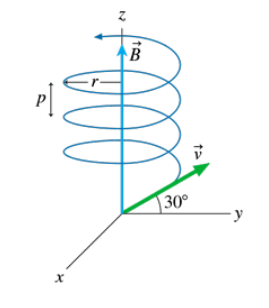
The uniform 30 mT magnetic field in FIGURE P29.65 points in the positive z-direction. An electron enters the region of magnetic field with a speed of 5.0 x 10⁶ m/s and at an angle of 30° above the xy-plane. Find the radius r and the pitch p of the electron's spiral trajectory.

Particle accelerators, such as the Large Hadron Collider, use magnetic fields to steer charged particles around a ring. Consider a proton ring with 36 identical bending magnets connected by straight segments. The protons move along a 1.0-m-long circular arc as they pass through each magnet. What magnetic field strength is needed in each magnet to steer protons around the ring with a speed of 2.5 x 10⁷ m/s? Assume that the field is uniform inside the magnet, zero outside.

Controlled fusion is a possible future energy source that would harness the same nuclear fusion reactions that power the sun. The simplest fusion reaction is ²H⁺ + ²H⁺ → ³He⁺⁺ + n + energy, in which nuclei of two deuterium atoms fuse into a nucleus while ejecting a neutron and releasing a substantial amount of energy. Deuterium is not an element but is the name given to 'heavy hydrogen,' in which the nucleus is not simply a proton but a proton and a neutron, with atomic mass 2 u. Two positive deuterium nuclei, which repel each other, can get close enough to fuse only if they have very high speeds. This can be achieved by creating a plasma of ionized deuterium gas at a temperature of 1.0 x 10⁸ K. No material substance can contain a plasma at this temperature, so the idea is to contain the plasma with magnetic fields. Consider the simplest model of using a solenoid to confine the ions to cyclotron motion around the field lines. The plasma ions have a range of speeds, and it's necessary to contain all the ions with speeds up to three times the rms speed at the plasma temperature. What magnetic field strength is needed to keep the fastest ions in 20-cm-diameter cyclotron orbits? The actual magnetic fields are considerably more complex, but your answer is a reasonable estimate of the required field strengths.

A proton moves in the uniform fields E = 2500 k V/m and B = 0.50 k T. At t = 0 s the proton is moving in a 1.0-cm-diameter circle in the xy-plane. How many revolutions will the proton have made during this time interval?

It is shown in more advanced courses that charged particles in circular orbits radiate electromagnetic waves, called cyclotron radiation. As a result, a particle undergoing cyclotron motion with speed v is actually losing kinetic energy at the rate$\frac{dK}{dt}=-\left(\frac{{\mu }_0{q}^4}{6\pi c{m}^2}\right)B^2{v}^2$

How long does it take (a) an electron and (b) a proton to radiate away half its energy while spiraling in a 2.0 T magnetic field?

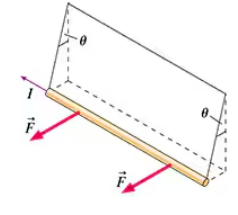
In FIGURE P29.75, a long, straight, current-carrying wire of linear mass density μ is suspended by threads. A magnetic field perpendicular to the wire exerts a horizontal force that deflects the wire to an equilibrium angle θ. Find an expression for the strength and direction of the magnetic field B.

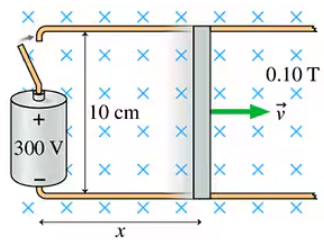
An electromagnetic rail gun uses magnetic forces to launch projectiles. FIGURE P29.76 shows a 10-cm-long, 10 g metal wire that can slide without friction along 1.0-m-long horizontal rails. The rails are connected to a 300 V source, and a 0.10 T magnetic field fills the space between the rails. Each rail has linear resistivity ⋋ = 0.10 Ω/m, which means that the resistance is ⋋ multiplied by the length of rail through which current flows. Assume that the sliding wire and the left end, where the voltage source is, have zero resistance. The wire is initially placed at x₀ = 5.0 cm then the switch is closed. What is the wire's speed as it leaves the rails?

A wire along the x-axis carries current I in the negative x-direction through the magnetic field . Find an expression for the net torque on the wire about the point x = 0.

A scientist measuring the resistivity of a new metal alloy left her ammeter in another lab, but she does have a magnetic field probe. So she creates a 6.5-m-long, 2.0-mm-diameter wire of the material, connects it to a 1.5 V battery, and measures a 3.0 mT magnetic field 1.0 mm from the surface of the wire. What is the material's resistivity?

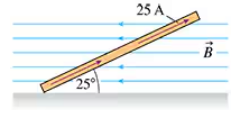
FIGURE CP29.79 is an edge view of a 2.0 kg square loop, 2.5 m on each side, with its lower edge resting on a frictionless, horizontal surface. A 25 A current is flowing around the loop in the direction shown. What is the strength of a uniform, horizontal magnetic field for which the loop is in static equilibrium at the angle shown?

Determine the field strength at the center of a current-carrying square loop having sides of length 2R.

A long, straight conducting wire of radius R has a nonuniform current density J = J₀r/R, where J₀ is a constant. The wire carries total current I. Find an expression for the magnetic field strength inside the wire at radius r.

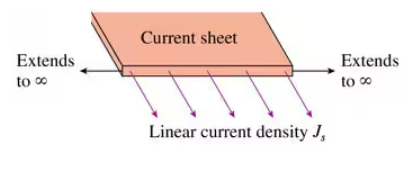
An infinitely wide flat sheet of charge flows out of the figure in FIGURE CP29.83. The current per unit width along the sheet (amps per meter) is given by the linear current density J_s. Find the magnetic field strength at distance d above or below the current sheet.