Back
BackProblem 1
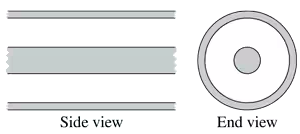
FIGURE EX24.1 shows two cross sections of two infinitely long coaxial cylinders. The inner cylinder has a positive charge, the outer cylinder has an equal negative charge. Draw this figure on your paper, then draw electric field vectors showing the shape of the electric field.
Problem 2
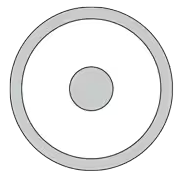
FIGURE EX24.2 shows a cross section of two concentric spheres. The inner sphere has a negative charge. The outer sphere has a positive charge larger in magnitude than the charge on the inner sphere. Draw this figure on your paper, then draw electric field vectors showing the shape of the electric field.
Problem 3
FIGURE EX24.3 shows a cross section of two infinite parallel planes of charge. Draw this figure on your paper, then draw electric field vectors showing the shape of the electric field.
Problem 4
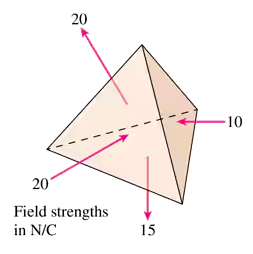
The electric field is constant over each face of the tetrahedron shown in FIGURE EX24.4. Does the box contain positive charge, negative charge, or no charge? Explain.
Problem 7
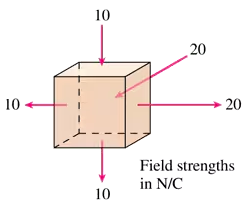
The cube in FIGURE EX24.7 contains negative charge. The electric field is constant over each face of the cube. Does the missing electric field vector on the front face point in or out? What strength must this field exceed?
Problem 10
The electric flux through the surface shown in FIGURE EX24.10 is 25 N m²/C. What is the electric field strength?
Problem 12b
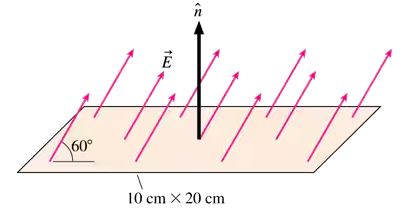
A 2.0 cm × 3.0 cm rectangle lies in the -plane with unit vector pointing in the +y-direction. What is the electric flux through the rectangle if the electric field is N/C?
Problem 14
A 12 cm × 12 cm rectangle lies in the first quadrant of the xy-plane with one corner at the origin. Unit vector points in the +𝒵-direction. What is the electric flux through the rectangle if the electric field is N/C? Hint: Divide the rectangle into narrow strips of width.
Problem 18
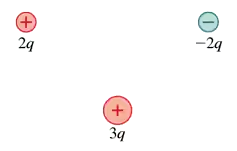
FIGURE EX24.18 shows three charges. Draw these charges on your paper four times. Then draw two-dimensional cross sections of three-dimensional closed surfaces through which the electric flux is (a) , (b) , (c) 0, and (d) .
Problem 21
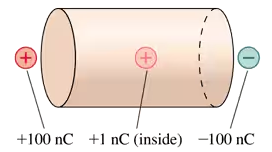
What is the net electric flux through the cylinder of FIGURE EX24.21?
Problem 25a
A thin, horizontal, 10-cm-diameter copper plate is charged to 3.5 nC. If the charge is uniformly distributed on the surface, what are the strength and direction of the electric field 0.1 mm above the center of the top surface of the plate?
Problem 26
A spark occurs at the tip of a metal needle if the electric field strength exceeds N/C, the field strength at which air breaks down. What is the minimum surface charge density for producing a spark?
Problem 29
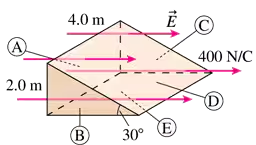
Find the electric fluxes ΦA to ΦE through surfaces A to E in FIGURE P24.29.
Problem 31
A 10 nC charge is at the center of a 2.0 m x 2.0 m x 2.0 m cube. What is the electric flux through the top surface of the cube?
Problem 32
Charges and are located at and , respectively. What is the net electric flux through a sphere of radius centered (a) at the origin and (b) at ?
Problem 34b
A spherically symmetric charge distribution produces the electric field N/C, where r is in m. How much charge is inside this 40-cm-diameter spherical surface?
Problem 36b
A 20-cm-radius ball is uniformly charged to 80 nC. How much charge is enclosed by spheres of radii 5, 10, and 20 cm?
Problem 38
The earth has a vertical electric field at the surface, pointing down, that averages 100 N/C. This field is maintained by various atmospheric processes, including lightning. What is the excess charge on the surface of the earth?
Problem 39
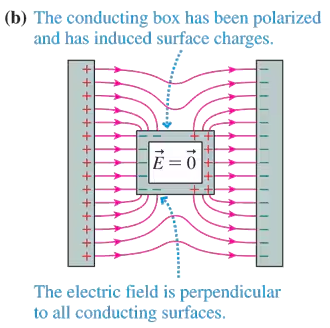
Figure 24.32b showed a conducting box inside a parallel-plate capacitor. The electric field inside the box is . Suppose the surface charge on the exterior of the box could be frozen. Draw a picture of the electric field inside the box after the box, with its frozen charge, is removed from the capacitor. Hint: Superposition.
Problem 41
An infinitely wide, horizontal metal plate lies above a horizontal infinite sheet of charge with surface charge density 800 nC/m2. The bottom surface of the plate has surface charge density -100 nC/m2. What is the surface charge density on the top surface of the plate?
Problem 44
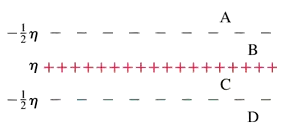
The three parallel planes of charge shown in FIGURE P24.44 have surface charge densities ─ ½ η , η , and ─ ½ η. Find the electric fields to in regions A to D. The upward direction is the + y-direction.
Problem 45b
An infinite slab of charge of thickness 2𝒵₀ lies in the xy-plane between 𝒵 = -𝒵₀ and 𝒵 = +𝒵₀ . The volume charge density p (C/m3) is a constant. Find an expression for the electric field strength above the slab (𝒵 ≥ 𝒵₀).
Problem 46
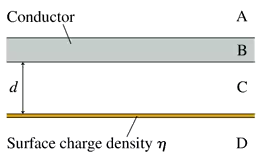
FIGURE P24.46 shows an infinitely wide conductor parallel to and distance d from an infinitely wide plane of charge with surface charge density η. What are the electric fields to in regions A to D?
Problem 48
An infinite slab of charge is centered in the xy-plane. It has charge density , where ρ₀ and z₀ are constants. This is a charge density that decreases exponentially as you move away from z = 0 in either the positive or negative direction. Find the electric field strength at distance z from the center of the slab.
Problem 55c
An early model of the atom, proposed by Rutherford after his discovery of the atomic nucleus, had a positive point charge + Ze (the nucleus) at the center of a sphere of radius R with uniformly distributed negative charge -Ze. Z is the atomic number, the number of protons in the nucleus and the number of electrons in the negative sphere. A uranium atom has Z = 92 and 𝑅 = 0.10nm . What is the electric field strength at r = ½𝑅?
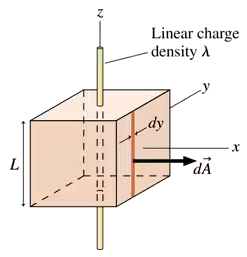
Problem 57a
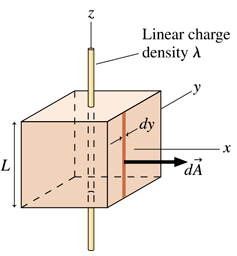
All examples of Gauss’s law have used highly symmetric surfaces where the flux integral is either zero or EA. Yet we’ve claimed that the net is independent of the surface. This is worth checking. FIGURE CP24.57 shows a cube of edge length L centered on a long thin wire with linear charge density λ. The flux through one face of the cube is not simply EA because, in this case, the electric field varies in both strength and direction. But you can calculate the flux by actually doing the flux integral. Consider the face parallel to the yz-plane. Define area as a strip of width dy and height L with the vector pointing in the 𝓍-direction. One such strip is located at position y. Use the known electric field of a wire to calculate the electric flux dΦ through this little area. Your expression should be written in terms of y, which is a variable, and various constants. It should not explicitly contain any angles.
Problem 57b
All examples of Gauss’s law have used highly symmetric surfaces where the flux integral is either zero or EA. Yet we’ve claimed that the net Φₑ = Qᵢₙ / ϵ₀ is independent of the surface. This is worth checking. FIGURE CP24.57 shows a cube of edge length L centered on a long thin wire with linear charge density λ. The flux through one face of the cube is not simply EA because, in this case, the electric field varies in both strength and direction. But you can calculate the flux by actually doing the flux integral. Now integrate dΦ to find the total flux through this face.
Problem 57c
All examples of Gauss’s law have used highly symmetric surfaces where the flux integral is either zero or EA. Yet we’ve claimed that the net is independent of the surface. This is worth checking. FIGURE CP24.57 shows a cube of edge length L centered on a long thin wire with linear charge density λ. The flux through one face of the cube is not simply EA because, in this case, the electric field varies in both strength and direction. But you can calculate the flux by actually doing the flux integral. Show that the net flux through the cube is .
Problem 58b
An infinite cylinder of radius R has a linear charge density λ . The volume charge density (C/m³) within the cylinder (r ≤ R ) is p (r) = rp₀ / R, where p₀ is a constant to be determined. The charge within a small volume dV is dq = pdV. The integral of pdV over a cylinder of length L is the total charge Q = λL within the cylinder. Use this fact to show that p₀ = 3λ / 2πR² Hint: Let dV be a cylindrical shell of length L, radius r, and thickness dr. What is the volume of such a shell?
Problem 58c
An infinite cylinder of radius R has a linear charge density λ. The volume charge density (C/m3) within the cylinder (r ≤ R) is , where p₀ is a constant to be determined. Use Gauss’s law to find an expression for the electric field strength E inside the cylinder, r ≤ R, in terms of λ and R.