Back
BackProblem 39
A 75 kg man weighs himself at the north pole and at the equator. Which scale reading is higher? By how much? Assume the earth is spherical.
Problem 40a
An object of mass m swings in a horizontal circle on a string of length L that tilts downward at angle θ. Find an expression for the angular velocity ω.
Problem 41
A concrete highway curve of radius 70 m is banked at a 15° angle. What is the maximum speed with which a 1500 kg rubber-tired car can take this curve without sliding?
Problem 43
A 4.4-cm-diameter, 24 g plastic ball is attached to a 1.2-m-long string and swung in a vertical circle. The ball's speed is 6.1 m/s at the point where it is moving straight up. What is the magnitude of the net force on the ball? Air resistance is not negligible.
Problem 45a
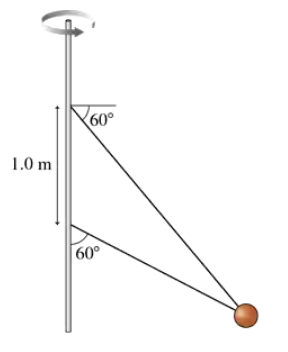
Two wires are tied to the 2.0 kg sphere shown in FIGURE P8.45. The sphere revolves in a horizontal circle at constant speed. For what speed is the tension the same in both wires?
Problem 47c
A 2.0 kg pendulum bob swings on a 2.0-m-long string. The bob's speed is 1.5 m/s when the string makes a 15° angle with vertical and the bob is moving toward the bottom of the arc. At this instant, what are the magnitudes of the tension in the string?
Problem 48b
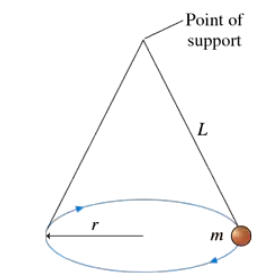
A conical pendulum is formed by attaching a ball of mass m to a string of length L, then allowing the ball to move in a horizontal circle of radius r. FIGURE P8.48 shows that the string traces out the surface of a cone, hence the name. Find an expression for the ball's angular speed ω.
Problem 51b
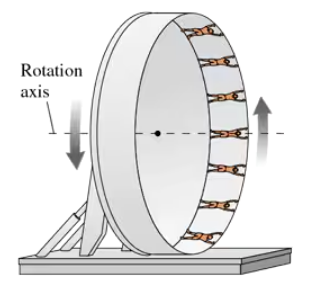
In an amusement park ride called The Roundup, passengers stand inside a 16-m-diameter rotating ring. After the ring has acquired sufficient speed, it tilts into a vertical plane, as shown in FIGURE P8.51. What is the longest rotation period of the wheel that will prevent the riders from falling off at the top?
Problem 52a
Suppose you swing a ball of mass m in a vertical circle on a string of length L. As you probably know from experience, there is a minimum angular velocity ωmin you must maintain if you want the ball to complete the full circle without the string going slack at the top. Find an expression for ωmin.
Problem 53
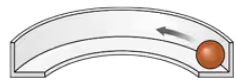
A 30 g ball rolls around a 40-cm-diameter L-shaped track, shown in FIGURE P8.53, at 60 rpm. What is the magnitude of the net force that the track exerts on the ball? Rolling friction can be neglected. Hint: The track exerts more than one force on the ball.
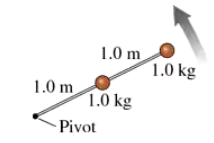
Problem 54
FIGURE P8.54 shows two small 1.0 kg masses connected by massless but rigid 1.0-m-long rods. What is the tension in the rod that connects to the pivot if the masses rotate at 30 rpm in a horizontal circle?
Problem 55a
The physics of circular motion sets an upper limit to the speed of human walking. (If you need to go faster, your gait changes from a walk to a run.) If you take a few steps and watch what's happening, you'll see that your body pivots in circular motion over your forward foot as you bring your rear foot forward for the next step. As you do so, the normal force of the ground on your foot decreases and your body tries to 'lift off' from the ground. A person's center of mass is very near the hips, at the top of the legs. Model a person as a particle of mass m at the top of a leg of length L. Find an expression for the person's maximum walking speed vmax.
Problem 56a
An airplane feels a lift force perpendicular to its wings. In level flight, the lift force points straight up and is equal in magnitude to the gravitational force on the plane. When an airplane turns, it banks by tilting its wings, as seen from behind, by an angle from horizontal. This causes the lift to have a radial component, similar to a car on a banked curve. If the lift had constant magnitude, the vertical component of would now be smaller than the gravitational force, and the plane would lose altitude while turning. However, you can assume that the pilot uses small adjustments to the plane's control surfaces so that the vertical component of continues to balance the gravitational force throughout the turn. Find an expression for the banking angle needed to turn in a circle of radius while flying at constant speed .
Problem 58
A 100 g ball on a 60-cm-long string is swung in a vertical circle about a point 200 cm above the floor. The string suddenly breaks when it is parallel to the ground and the ball is moving upward. The ball reaches a height 600 cm above the floor. What was the tension in the string an instant before it broke?
Problem 60a
Scientists design a new particle accelerator in which protons (mass 1.7 X 10-27 kg) follow a circular trajectory given by where c = 5.0 m and k = 8.0 x 104 rad/s2 are constants and t is the elapsed time. What is the radius of the circle?
Problem 62a
2.0 kg ball swings in a vertical circle on the end of an 80-cm-long string. The tension in the string is 20 N when its angle from the highest point on the circle is θ = 30°. What is the ball's speed when θ = 30°?
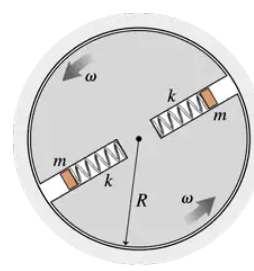
Problem 63
For safety, elevators have a rotational governor, a device that is attached to and rotates with one of the elevator's pulleys. The governor, shown in FIGURE P8.63, is a disk with two hollow channels holding springs with metal blocks of mass m attached to their free ends. The faster the governor spins, the more the springs stretch. At a critical angular velocity ωc, the metal blocks contact the housing, which completes a circuit and activates an emergency brake. The spring force on a mass, which we will explore more thoroughly in Chapter 9, is FSp = k(r - L), where k is the spring constant measured in N/m, and L is the relaxed (unstretched) length of the spring. Suppose a rotational governor has L = 0.80R and the emergency brake activates when the metal blocks reach r = R. What is the critical angular velocity in rpm if R = 15cm, k = 20 N/m, and m = 25g? Ignore gravity.
Problem 68a
In the absence of air resistance, a projectile that lands at the elevation from which it was launched achieves maximum range when launched at a 45° angle. Suppose a projectile of mass m is launched with speed into a headwind that exerts a constant, horizontal retarding force . Find an expression for the angle at which the range is maximum.
Problem 68b
In the absence of air resistance, a projectile that lands at the elevation from which it was launched achieves maximum range when launched at a 45° angle. Suppose a projectile of mass m is launched with speed into a headwind that exerts a constant, horizontal retarding force By what percentage is the maximum range of a 0.50 kg ball reduced if ?
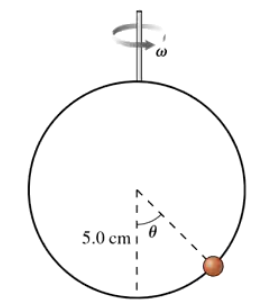
Problem 69a
The 10 mg bead in FIGURE CP8.69 is free to slide on a frictionless wire loop. The loop rotates about a vertical axis with angular velocity ω. If ω is less than some critical value ω꜀, the bead sits at the bottom of the spinning loop. When ω > ω꜀, the bead moves out to some angle θ. What is ω꜀ in rpm for the loop shown in the figure?
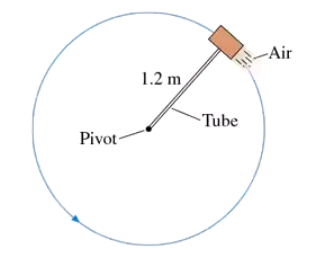
Problem 70
A 500 g steel block rotates on a steel table while attached to a 1.2-m-long hollow tube as shown in FIGURE CP8.70. Compressed air fed through the tube and ejected from a nozzle on the back of the block exerts a thrust force of 4.0 N perpendicular to the tube. The maximum tension the tube can withstand without breaking is 50 N. If the block starts from rest, how many revolutions does it make before the tube breaks?
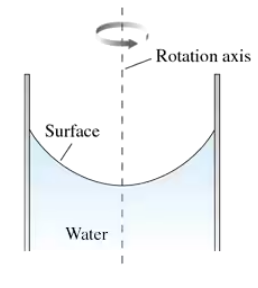
Problem 72
If a vertical cylinder of water (or any other liquid) rotates about its axis, as shown in FIGURE CP8.72, the surface forms a smooth curve. Assuming that the water rotates as a unit (i.e., all the water rotates with the same angular velocity), show that the shape of the surface is a parabola described by the equation z = (ω2 / 2g) r2. Hint: Each particle of water on the surface is subject to only two forces: gravity and the normal force due to the water underneath it. The normal force, as always, acts perpendicular to the surface.