Back
BackProblem 6
We saw earlier (Chapter 19) that the rate energy reaches the Earth from the Sun (the “solar constant”) is about 1.3 x 10³ W/m². What is (a) the apparent brightness b of the Sun, and (b) the intrinsic luminosity L of the Sun?
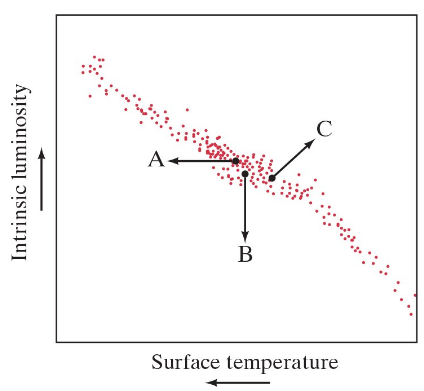
Problem 16
(II) Suppose that three main-sequence stars could undergo the three changes represented by the three arrows, A, B, and C, in the H–R diagram of Fig. 44–35. For each case, describe the changes in temperature, intrinsic luminosity, and size.
Problem 27
If a galaxy is traveling away from us at 2.2% of the speed of light, roughly how far away is it?
Problem 36
Starting from Eq. 44–3, show that the Doppler shift in wavelength is ∆λ/λᵣₑₛₜ ≈ v/c (Eq. 44–6) for v ≪ c. [Hint: Use the binomial expansion.]
Problem 39
Calculate the peak wavelength of the CMB at 1.0 s after the birth of the universe. In what part of the EM spectrum is this radiation?
Problem 42
At approximately what time had the universe cooled below the threshold temperature for producing (a) kaons (M ≈ 500 MeV/ c²), (b) Y (M ≈ 9500 MeV/c²), and (c) muons (M ≈ 100 MeV/c²)?
Problem 52
(a) In order to measure distances with parallax at 100 ly, what minimum angular resolution (in degrees) is needed?
(b) What diameter mirror or lens would be needed?
Problem 63b
Use special relativity and Newton’s law of gravitation to show that a photon of mass m = E/c² just grazing the Sun will be deflected by an angle ∆θ given by ∆θ = 2GM/c²R, where G is the gravitational constant, R and M are the radius and mass of the Sun, and c is the speed of light. Put in values and show ∆θ = 0.87". (General Relativity predicts an angle twice as large, 1.74".)
Problem 66
Determine the radius of a neutron star using the same argument as in Problem 65 but for N neutrons only. Show that the radius of a neutron star, of 1.5 solar masses, is about 11 km.