Back
BackProblem 12
What minimum radius must a large conducting sphere (of an electrostatic generating machine) have if it is to be at 45,000 V without discharge into the air? How much charge will it carry?
Problem 19
Suppose the end of your finger is charged.
(a) Estimate the breakdown voltage in air for your finger.
(b) About what surface charge density would have to be on your finger at this voltage?
Problem 23
A very long conducting cylinder (length ℓ) of radius R₀ (R₀ ≪ ℓ) carries a uniform surface charge density σ (C/m²). The cylinder is at an electric potential V₀. Determine the potential, at points far from the end, at a distance R from the center of the cylinder for
(a) R > R₀
(b) R < R₀.
(c) Is V = 0 at R = ∞ (assume ℓ = ∞ )? Explain. [Hint: Recall Gauss’s law.]
Problem 26
Two point charges, 3.4 μC and -2.0 μC, are placed 8.0 cm apart on the x axis. At what points along the x axis are
(a) the electric field zero and
(b) the potential zero? Let V = 0 at r = ∞.
Problem 38
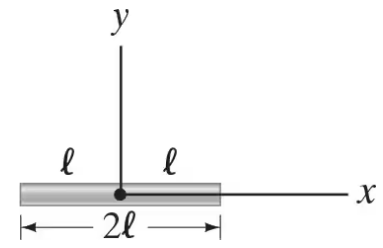
A thin rod of length 2ℓ is centered on the x axis as shown in Fig. 23–46. The rod carries a uniformly distributed charge Q. Determine the potential V as a function of y for points along the y axis. Let V = 0 at infinity.
Problem 44
A metal sphere of radius r₀ = 0.35 m carries a charge Q = 0.50 μC. Equipotential surfaces are to be drawn for 100-V intervals outside the sphere. Determine the radius r of the first equipotential from the surface.
Problem 45
Calculate the electric potential due to a tiny dipole whose dipole moment is 4.8 x 10⁻³⁰ Cm at a point 4.1 x 10⁻⁹ m away if this point is along the axis of the dipole nearer the positive charge.
Problem 45b
Calculate the electric potential due to a tiny dipole whose dipole moment is 4.8 x 10⁻³⁰ Cm at a point 4.1 x 10⁻⁹ m away if this point is 45° above the axis but nearer the positive charge.
Problem 52
A dust particle with mass of 0.050 g and a charge of 2.0 x 10⁻⁶ C is in a region of space where the potential is given by V(x) = (2.0 V/m²) x² - (3.0 V/m³)x³. If the particle starts at x = 2.5m, what is the initial acceleration of the charge?
Problem 71a
An analog voltage signal can vary from 0 V to 5.00 V, and it is to be converted to an 8-bit binary representation. What voltage, to the nearest 0.01 V, would have a binary representation of 01110101?
Problem 71b
An analog voltage signal can vary from 0 V to 5.00 V, and it is to be converted to an 8-bit binary representation. What binary number would best represent 3.47 volts?
Problem 83a
Two point charges are fixed 4.0 cm apart from each other. Their charges are Q₁ = Q₂ = 6.5 μC and their masses are m₁ = 2.5 mg and m₂ = 3.5 mg. If Q₁ is released from rest, what will be its speed after a very long time?
Problem 85
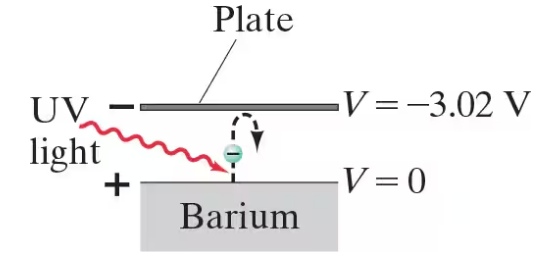
In a photocell, ultraviolet (UV) light provides enough energy to some electrons in barium metal to eject them from the surface at high speed. To measure the maximum energy of the electrons, another plate above the barium surface is kept at a negative enough potential that the emitted electrons are slowed down and stopped, and return to the barium surface. See Fig. 23–52. If the plate voltage is -3.02 V (compared to the barium) when the fastest electrons are stopped, what was the speed of these electrons when they were emitted?
Problem 88
Near the surface of the Earth there is an electric field of about 150 V/m which points downward. Two identical balls with mass m = 0.550 kg are dropped from a height of 2.00 m, but one of the balls is positively charged with q₁ = 650 μC, and the second is negatively charged with q₂ = -650 μC. Use conservation of energy to determine the difference in the speeds of the two balls when they hit the ground. (Neglect air resistance.)
Problem 98
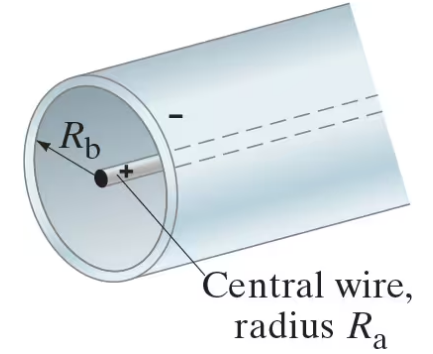
A Geiger counter is used to detect charged particles emitted by radioactive nuclei. It consists of a thin, positively charged central wire of radius Rₐ surrounded by a concentric conducting cylinder of radius Rᵦ with an equal negative charge (Fig. 23–57). The charge per unit length on the inner wire is λ (units C/m). The interior space between wire and cylinder is filled with low-pressure inert gas. Charged particles ionize some of these gas atoms; the resulting free electrons are attracted toward the positive central wire. If the radial electric field is strong enough, the freed electrons gain enough energy to ionize other atoms, causing an “avalanche” of electrons to strike the central wire, generating an electric “signal.” Find the expression for the electric field between the wire and the cylinder, and (b) show that the potential difference between Rₐ and Rᵦ is Vₐ - Vᵦ = ( λ / 2π∊₀ ) ln( Rᵦ/Rₐ) .
Problem 100
The liquid-drop model of the nucleus suggests that high-energy oscillations of certain nuclei can split (“fission”) a large nucleus into two unequal fragments plus a few neutrons. Using this model, consider the case of a uranium nucleus fissioning into two spherical fragments, one with a charge q₁ = +38e and radius r₁ = 5.5 x 10⁻¹⁵ m, the other with q₂ = + 54e and r₂ = 6.2 x 10⁻¹⁵ m. Calculate the electric potential energy (MeV) of these fragments, assuming that the charge is uniformly distributed throughout the volume of each spherical nucleus and that their surfaces are initially in contact at rest. The electrons surrounding the nuclei can be neglected. This electric potential energy will then be entirely converted to kinetic energy as the fragments repel each other. How does your predicted kinetic energy of the fragments agree with the observed value associated with uranium fission (approximately 200 MeV total)? [ 1 MeV = 10⁶ eV.]
Problem 101
A thin flat disk of radius R₀ carries a total charge Q that is distributed uniformly over its surface. The electric potential at a distance x on the x axis is given by V(x) = Q/ 2π∊₀R₀²[(x² + R²₀) ¹⸍² - x]. (See Example 23–10.) Show that the electric field at a distance x on the x axis is given by E(x) = Q/2π∊₀R₀² ( 1 - ( x / ( x² + R²₀))¹⸍². Make graphs of V(x) and E(x) as a function of x/R₀ for x/R₀ = 0 to 4. (Do the calculations in steps of 0.1.) Use Q = 5.0μC and R₀ = 10 cm for the calculation and graphs.
Problem 103a
Inside a high-voltage lab, engineers have designed a storage container for electrical energy using a nonconducting sphere of radius r2 that contains a concentric spherical cavity of radius r1. The material between r₁ and r₂ carries a uniform charge density ρE ( C/m³). Determine the electric potential V, relative to V = 0 at r = ∞, as a function of the distance r from the center for r > r₂.
Problem 105a
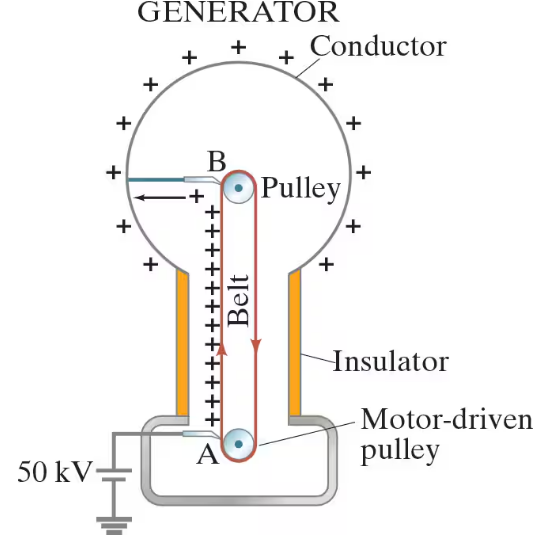
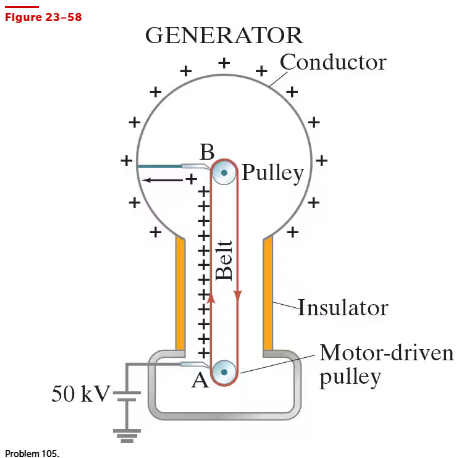
A Van de Graaff generator (Fig. 23–58) can develop a very large potential difference, even millions of volts. Electrons are pulled off the belt by the high voltage pointed electrode (positive) at A, leaving the belt positively charged. (Recall Example 23–5 where we saw that near sharp points the electric field is high and ionization can occur.) The belt carries the positive charge up inside the spherical shell where electrons from the large conducting sphere are attracted over to the pointed conductor at B, leaving the outer surface of the conducting sphere positively charged. As more charge is brought up, the sphere reaches extremely high voltage. Consider a Van de Graaff generator with a sphere of radius 0.20 m. What is the electric potential on the surface of the sphere when electrical breakdown occurs ( E = 3 x 10⁶ V/m) ? Assume V = 0 at r = ∞.
Problem 105b
A Van de Graaff generator (Fig. 23–58) can develop a very large potential difference, even millions of volts. Electrons are pulled off the belt by the high voltage pointed electrode (positive) at A, leaving the belt positively charged. (Recall Example 23–5 where we saw that near sharp points the electric field is high and ionization can occur.) The belt carries the positive charge up inside the spherical shell where electrons from the large conducting sphere are attracted over to the pointed conductor at B, leaving the outer surface of the conducting sphere positively charged. As more charge is brought up, the sphere reaches extremely high voltage. Consider a Van de Graaff generator with a sphere of radius 0.20 m.
(b) What is the charge on the sphere for the potential found in part (a)