Here are the essential concepts you must grasp in order to answer the question correctly.
Dissociation of Acids
Dissociation refers to the process by which an acid separates into its constituent ions in solution. For weak acids like HNO2, this process is not complete, meaning only a fraction of the acid molecules dissociate into hydrogen ions (H+) and nitrite ions (NO2-). Understanding the degree of dissociation is crucial for calculating properties such as freezing point depression.
Recommended video:
Acid-Base Dissociation Example
Freezing Point Depression
Freezing point depression is a colligative property that describes how the freezing point of a solvent decreases when a solute is added. The extent of this depression depends on the number of solute particles in solution, which can be calculated using the formula ΔTf = i * Kf * m, where 'i' is the van 't Hoff factor, 'Kf' is the freezing point depression constant, and 'm' is the molality of the solution.
Recommended video:
Freezing Point Depression
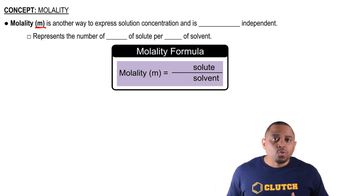
Molality
Molality is a measure of concentration defined as the number of moles of solute per kilogram of solvent. It is expressed in moles per kilogram (mol/kg) and is particularly useful in colligative property calculations because it remains unaffected by temperature changes. In this problem, calculating the molality of the HNO2 solution is essential for determining the extent of freezing point depression and, subsequently, the fraction of dissociated HNO2.
Recommended video:

 Verified step by step guidance
Verified step by step guidance