Skip to main content
Pearson+ LogoPearson+ Logo
Ch.15 - Chemical Kinetics
All textbooksTro 6th EditionCh.15 - Chemical KineticsProblem 99
Chapter 15, Problem 99

The reaction AB(aq) → A(g) + B(g) is second order in AB and has a rate constant of 0.0118 M^-1 s^-1 at 25.0 °C. A reaction vessel initially contains 250.0 mL of 0.100 M AB that is allowed to react to form the gaseous product. The product is collected over water at 25.0 °C. How much time is required to produce 200.0 mL of the products at a barometric pressure of 755.1 mmHg? (The vapor pressure of water at this temperature is 23.8 mmHg.)

Verified step by step guidance
1
Identify the initial concentration of AB, which is 0.100 M, and the initial volume of the solution, which is 250.0 mL.
Use the ideal gas law to determine the moles of gas produced. First, calculate the pressure of the gas by subtracting the vapor pressure of water from the barometric pressure: \( P_{gas} = 755.1 \text{ mmHg} - 23.8 \text{ mmHg} \).
Convert the volume of the gas produced (200.0 mL) to liters and use the ideal gas law \( PV = nRT \) to find the moles of gas, where \( R = 0.0821 \text{ L atm K}^{-1} \text{ mol}^{-1} \) and \( T = 298 \text{ K} \).
Determine the change in concentration of AB using the stoichiometry of the reaction and the moles of gas produced. Since the reaction is second order, use the integrated rate law for a second-order reaction: \( \frac{1}{[AB]_t} = \frac{1}{[AB]_0} + kt \).
Solve for the time \( t \) using the integrated rate law, where \( k = 0.0118 \text{ M}^{-1} \text{ s}^{-1} \), \([AB]_0 = 0.100 \text{ M}\), and \([AB]_t\) is the concentration of AB after the reaction.

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Reaction Order

The order of a reaction indicates how the rate of the reaction depends on the concentration of the reactants. In this case, the reaction is second order in AB, meaning that the rate is proportional to the square of the concentration of AB. Understanding reaction order is crucial for determining how changes in concentration affect the rate and for applying the appropriate rate laws to calculate time or concentration changes.
Recommended video:
Guided course
00:36
Average Bond Order

Rate Constant

The rate constant (k) is a proportionality factor in the rate law that relates the rate of a reaction to the concentrations of the reactants. For a second-order reaction, the units of k are M^-1 s^-1. The value of the rate constant is temperature-dependent, and knowing it allows for the calculation of the reaction rate and the time required to reach a certain concentration of products.
Recommended video:
Guided course
00:45
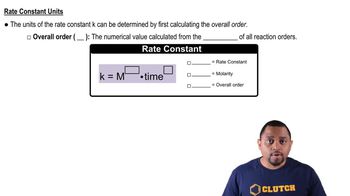
Rate Constant Units

Gas Laws and Vapor Pressure

Gas laws describe the behavior of gases under various conditions of temperature and pressure. In this scenario, the vapor pressure of water at 25.0 °C must be considered when calculating the volume of gaseous products collected over water. The total pressure of the gas collected is the sum of the partial pressures of the gas and the water vapor, which is essential for determining the actual volume of the gaseous products produced.
Recommended video:
Guided course
02:40
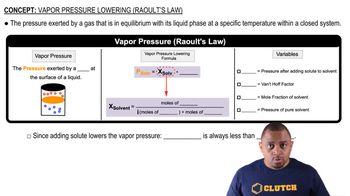
Raoult's Law and Vapor Pressure
Related Practice
Textbook Question

Dinitrogen pentoxide decomposes in the gas phase to form nitrogen dioxide and oxygen gas. The reaction is first order in dinitrogen pentoxide and has a half-life of 2.81 h at 25 °C. If a 1.5-L reaction vessel initially contains 745 torr of N2O5 at 25 °C, what partial pressure of O2 is present in the vessel after 215 minutes?

1
views
Textbook Question

Iodine atoms combine to form I2 in liquid hexane solvent with a rate constant of 1.5⨉1010 L/mols. The reaction is second order in I. Since the reaction occurs so quickly, the only way to study the reaction is to create iodine atoms almost instantaneously, usually by photochemical decomposition of I2. Suppose a flash of light creates an initial [I] concentration of 0.0100 M. How long will it take for 95% of the newly created iodine atoms to recombine to form I2?

Textbook Question

Consider this energy diagram:

a. How many elementary steps are involved in this reaction?

Textbook Question

Consider this energy diagram:

d. Is the overall reaction endothermic or exothermic?