Ch.1 - Matter, Measurement & Problem Solving

Chapter 1, Problem 145
A cube has an edge length of 7 cm. If it is divided up into 1 cm cubes, how many 1 cm cubes are there?
 Verified step by step guidance
Verified step by step guidance1
insert step 1> Calculate the volume of the original cube using the formula for the volume of a cube: \( V = a^3 \), where \( a \) is the edge length of the cube.
insert step 2> Substitute the given edge length of the cube (7 cm) into the formula: \( V = 7^3 \).
insert step 3> Calculate the volume of the original cube.
insert step 4> Since each smaller cube has a volume of \( 1^3 = 1 \) cm\(^3\), the number of smaller cubes is equal to the volume of the original cube.
insert step 5> Determine the number of 1 cm cubes by dividing the volume of the original cube by the volume of one smaller cube.
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Volume of a Cube
The volume of a cube is calculated using the formula V = a³, where 'a' is the length of one edge. For a cube with an edge length of 7 cm, the volume would be 7 cm × 7 cm × 7 cm, resulting in 343 cm³. This concept is essential for understanding how the total space within the cube can be quantified.
Recommended video:
Guided course
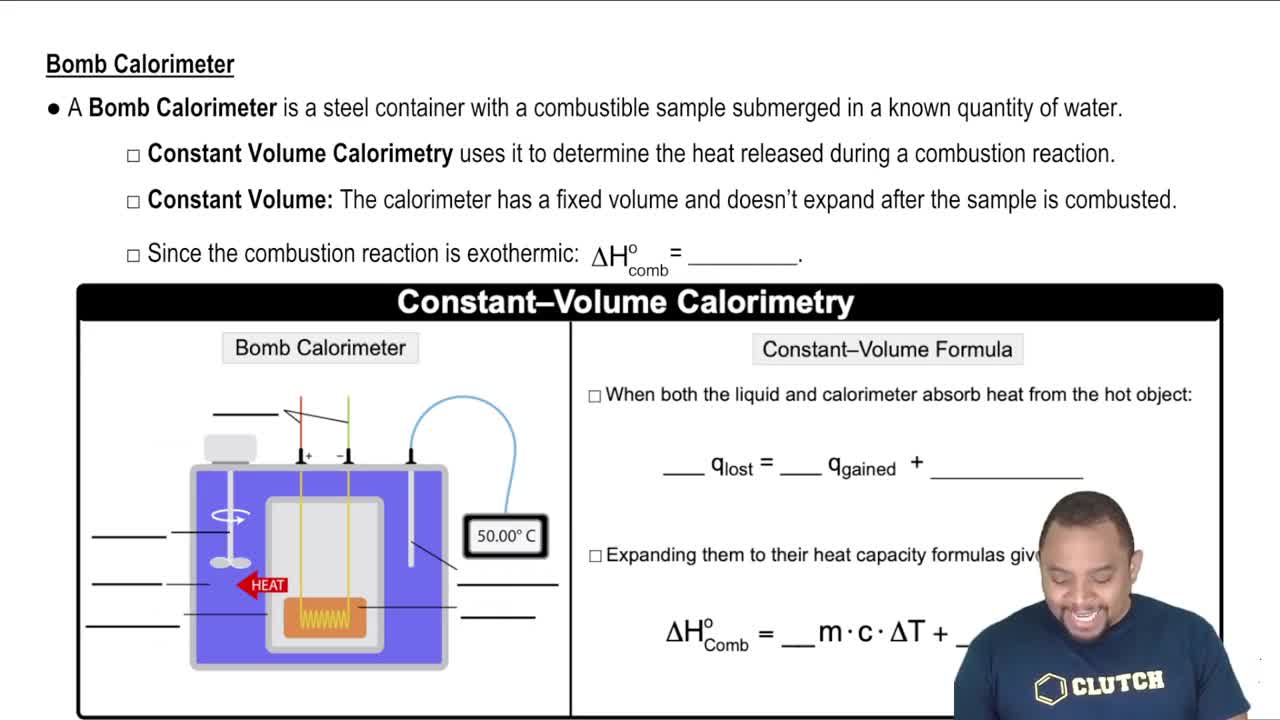
Constant-Volume Calorimetry
Unit Cubes
Unit cubes are the smallest cubes used to fill a larger volume, typically measuring 1 cm on each side. When determining how many unit cubes fit into a larger cube, the total volume of the larger cube is divided by the volume of a unit cube (1 cm³). This concept helps visualize and calculate the number of smaller cubes that can occupy the same space.
Recommended video:
Guided course

SI Units
Division of Volume
To find out how many smaller cubes fit into a larger cube, the total volume of the larger cube is divided by the volume of the smaller cube. In this case, dividing the volume of the 7 cm cube (343 cm³) by the volume of a 1 cm cube (1 cm³) gives the total number of 1 cm cubes. This division is a fundamental operation in determining how many discrete units can fit into a given space.
Recommended video:
Guided course

Scientific Notation in Multiplication and Division
Related Practice
