Textbook Question
Write the nuclear equation for the most likely mode of decay for each unstable nuclide. a. Kr-74 b. Th-221 c. Ar-44 d. Nb-85
Ch.20 - Radioactivity and Nuclear Chemistry
Chapter 20, Problem 83
Radium-226 (atomic mass = 226.025402 amu) decays to radon-222 (a radioactive gas) with a half-life of 1.6⨉103 years. What volume of radon gas (at 25.0 °C and 1.0 atm) does 25.0 g of radium produce in 5.0 days? (Report your answer to two significant digits.)
Verified step by step guidance1
Convert the mass of radium-226 to moles using its atomic mass: \( \text{moles of } \text{Ra} = \frac{25.0 \text{ g}}{226.025402 \text{ amu}} \).
Determine the fraction of radium that decays in 5.0 days using the half-life formula: \( N_t = N_0 \left( \frac{1}{2} \right)^{\frac{t}{t_{1/2}}} \), where \( t = 5.0 \text{ days} \) and \( t_{1/2} = 1.6 \times 10^3 \text{ years} \).
Calculate the moles of radon-222 produced, which is equal to the moles of radium-226 that decayed.
Use the ideal gas law \( PV = nRT \) to find the volume of radon gas, where \( P = 1.0 \text{ atm} \), \( R = 0.0821 \text{ L atm K}^{-1} \text{ mol}^{-1} \), and \( T = 25.0 \degree C = 298.15 \text{ K} \).
Solve for \( V \) in the ideal gas law equation to find the volume of radon gas produced.
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Radioactive Decay and Half-Life
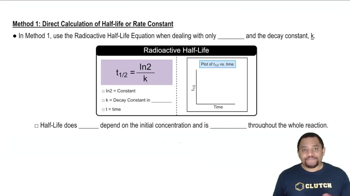
Radioactive decay is the process by which an unstable atomic nucleus loses energy by emitting radiation. The half-life is the time required for half of the radioactive atoms in a sample to decay. For Radium-226, with a half-life of 1.6 × 10^3 years, this means that after this period, half of the original amount will have transformed into Radon-222.
Recommended video:
Guided course
01:49
Method 1 of Radioactive Half-Life
Ideal Gas Law
The Ideal Gas Law relates the pressure, volume, temperature, and number of moles of a gas through the equation PV = nRT. Here, P is pressure, V is volume, n is the number of moles, R is the ideal gas constant, and T is temperature in Kelvin. This law is essential for calculating the volume of gas produced from the decay of Radium-226 into Radon-222 under specified conditions.
Recommended video:
Guided course
01:15Ideal Gas Law Formula
Stoichiometry of Radioactive Decay
Stoichiometry in the context of radioactive decay involves calculating the amount of product formed from a given amount of reactant based on the decay process. In this case, knowing the initial mass of Radium-226 allows us to determine how much Radon-222 is produced after a certain time, using the decay constant derived from the half-life.
Recommended video:
Guided course
03:00Rate of Radioactive Decay