One of the nuclides in spent nuclear fuel is U-235, an alpha emitter with a half-life of 703 million years. How long will it take for the amount of U-235 to reach 10.0% of its initial amount?

Verified step by step guidance

Identify the type of decay process: U-235 undergoes alpha decay, which is a first-order process.

Use the first-order decay formula: \( N_t = N_0 e^{-kt} \), where \( N_t \) is the remaining quantity, \( N_0 \) is the initial quantity, \( k \) is the decay constant, and \( t \) is time.

Determine the decay constant \( k \) using the half-life formula: \( k = \frac{\ln(2)}{\text{half-life}} \). Substitute the given half-life of 703 million years.

Set \( N_t = 0.10 N_0 \) to represent 10% of the initial amount and substitute into the decay formula: \( 0.10 N_0 = N_0 e^{-kt} \).

Solve for \( t \) by taking the natural logarithm of both sides and rearranging the equation: \( t = \frac{\ln(0.10)}{-k} \).

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.

Video duration:

Was this helpful?

Key Concepts

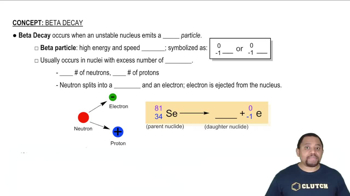
Here are the essential concepts you must grasp in order to answer the question correctly.

Half-Life

Half-life is the time required for half of the radioactive nuclei in a sample to decay. For U-235, with a half-life of 703 million years, this means that after this period, only half of the original amount remains. Understanding half-life is crucial for calculating the remaining quantity of a radioactive substance over time.

Exponential Decay

Exponential decay describes the process by which a quantity decreases at a rate proportional to its current value. In the context of radioactive decay, the amount of U-235 decreases exponentially over time, which can be mathematically represented by the equation N(t) = N0 * (1/2)^(t/T), where N0 is the initial amount, T is the half-life, and t is the elapsed time.

Radioactive Decay Calculation

To determine how long it takes for a radioactive substance to reach a specific percentage of its initial amount, one can use the formula derived from the half-life concept. For U-235 to reach 10% of its initial amount, we can set up the equation N(t) = 0.1 * N0 and solve for t, using the known half-life to find the time required for this decay.