Textbook Question
One of the nuclides in spent nuclear fuel is U-235, an alpha emitter with a half-life of 703 million years. How long will it take for the amount of U-235 to reach 10.0% of its initial amount?

 Verified step by step guidance
Verified step by step guidance
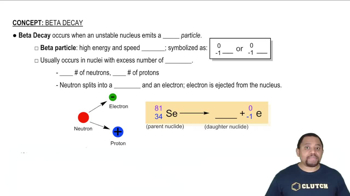
One of the nuclides in spent nuclear fuel is U-235, an alpha emitter with a half-life of 703 million years. How long will it take for the amount of U-235 to reach 10.0% of its initial amount?
A radioactive sample contains 1.55 g of an isotope with a halflife of 3.8 days. What mass of the isotope remains after 5.5 days?
A sample of F-18 has an initial decay rate of 1.5⨉105/s. How long will it take for the decay rate to fall to 2.5⨉103/s? (F-18 has a half-life of 1.83 hours.)