Skip to main content
Pearson+ LogoPearson+ Logo
Ch.21 - Transition Elements and Coordination Chemistry
All textbooksMcMurry 8th EditionCh.21 - Transition Elements and Coordination ChemistryProblem 21.121
Chapter 21, Problem 21.121

Predict the crystal field energy-level diagram for a linear ML2 complex that has two ligands along the :

Verified step by step guidance
1
Identify the geometry of the complex. In this case, the complex is described as linear with the formula ML2, indicating that the metal (M) is in the center with two ligands (L) aligned along the same axis.
Understand the coordination number and arrangement. For a linear ML2 complex, the coordination number is 2, which means there are two ligands directly coordinating with the metal ion.
Determine the splitting of the d-orbitals in the presence of the ligands. In a linear geometry, the d-orbitals split into different energy levels due to the electrostatic field created by the ligands. The d-orbitals along the axis of the ligands (d_z^2) will experience a different environment compared to those lying in the plane perpendicular to the axis (d_xy, d_xz, d_yz, d_x^2-y^2).
Predict the arrangement of the d-orbitals in terms of energy. In a linear complex, the d_z^2 orbital will have a higher energy due to direct interaction with the ligands along the z-axis. The other four d-orbitals (d_xy, d_xz, d_yz, d_x^2-y^2) will be lower in energy and are degenerate (having the same energy level) as they experience less direct interaction with the ligands.
Sketch the crystal field energy-level diagram based on the above predictions. Place the d_z^2 orbital at a higher energy level and group the other four d-orbitals together at a lower energy level, indicating their degeneracy and lesser interaction with the ligands.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.
Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Crystal Field Theory

Crystal Field Theory (CFT) explains how the arrangement of ligands around a central metal ion affects the energy levels of the d-orbitals. In a complex, ligands create an electric field that splits the degenerate d-orbitals into different energy levels, influencing the complex's stability, color, and magnetic properties.
Recommended video:
Guided course
01:18
The study of ligand-metal interactions helped to form Ligand Field Theory which combines CFT with MO Theory.

Ligand Field Strength

Ligand field strength refers to the ability of a ligand to influence the splitting of d-orbitals in a metal complex. Strong field ligands cause a larger splitting of the d-orbitals, leading to different electronic configurations and properties compared to weak field ligands, which result in smaller splitting.
Recommended video:
Guided course
02:40
Strong-Field Ligands result in a large Δ and Weak-Field Ligands result in a small Δ.

Geometry of Coordination Complexes

The geometry of coordination complexes, such as linear, tetrahedral, or octahedral, determines the spatial arrangement of ligands around the metal center. In a linear ML2 complex, the ligands are positioned 180 degrees apart, which affects the d-orbital splitting pattern and the overall electronic structure of the complex.
Recommended video:
Guided course
02:40
Molecular Geometry of Coordination Complexes
Related Practice
Textbook Question

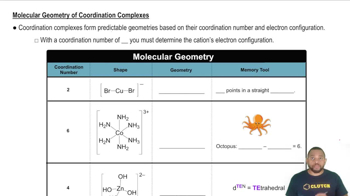
Draw a crystal field energy-level diagram, and predict the number of unpaired electrons for each of the following: 

(a) [Mn(H2O)6]2+

Textbook Question

Explain why [CoCl4]2- (blue) and [Co(H2O)6]2+ (pink) have different colors. Which complex has its absorption bands at longer wavelengths?

Textbook Question

Look at the colors of the isomeric complexes in Figure 21.12, and predict which is the stronger field ligand, nitro (-NO2) of nitrito (-ONO). Explain. 

Textbook Question

Predict the crystal field energy-level diagram for a square pyramidal ML5 complex that has two ligands along the axes but only one ligand along the z axis. Your diagram should be intermediate between those for an octahedral ML6 complex and a square planar ML4 complex.

Textbook Question

Give a valence bond description of the bonding in each of the following complexes. Include orbital diagrams for the free metal ion and the metal ion in the complex. Indicate which hybrid orbitals the metal ion uses for bonding, and specify the number of unpaired electrons. 

(b) [NiBr4]2- (tetrahedral) 

Textbook Question

For each of the following complexes, describe the bonding using valence bond theory. Include orbital diagrams for the free metal ion and the metal ion in the complex. Indicate which hybrid orbitals the metal ion uses for bonding, and specify the number of unpaired electrons. 

(a) [AuCl4]2 (square planar)