Textbook Question
The pH of a solution of NH3 and NH4Br is 8.90. What is the molarity of NH4Br if the molarity of NH3 is 0.016 M?
Ch.17 - Applications of Aqueous Equilibria
Chapter 17, Problem 59
The pH of a solution of HN3 (Ka = 1.9 x10^-5) and NaN3 is 4.86. What is the molarity of NaN3 if the molarity of HN3 is 0.016 M?
Verified step by step guidance1
Step 1: Recognize that the solution is a buffer solution, consisting of a weak acid (HN3) and its conjugate base (NaN3). Use the Henderson-Hasselbalch equation to find the relationship between pH, pKa, and the concentrations of the acid and its conjugate base.
Step 2: Calculate the pKa of HN3 using the given Ka value. The formula is \( \text{pKa} = -\log(\text{Ka}) \). Substitute \( \text{Ka} = 1.9 \times 10^{-5} \) into the formula to find pKa.
Step 3: Use the Henderson-Hasselbalch equation: \( \text{pH} = \text{pKa} + \log\left(\frac{[\text{A}^-]}{[\text{HA}]}\right) \), where \([\text{A}^-]\) is the concentration of the conjugate base (NaN3) and \([\text{HA}]\) is the concentration of the weak acid (HN3).
Step 4: Substitute the known values into the Henderson-Hasselbalch equation: \( \text{pH} = 4.86 \), \( \text{pKa} \) from Step 2, and \([\text{HA}] = 0.016 \text{ M}\). Solve for \([\text{A}^-]\), the concentration of NaN3.
Step 5: Rearrange the equation to solve for \([\text{A}^-]\): \( \log\left(\frac{[\text{A}^-]}{0.016}\right) = \text{pH} - \text{pKa} \). Use the antilog to find \([\text{A}^-]\), which is the molarity of NaN3.
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Acid-Base Equilibrium
Acid-base equilibrium involves the balance between an acid and its conjugate base in a solution. In this case, HN3 is a weak acid that partially dissociates in water, while NaN3 provides the conjugate base (N3-). The pH of the solution reflects the concentration of hydrogen ions, which is influenced by the ratio of the concentrations of the acid and its conjugate base.
Recommended video:
Guided course
05:11
Triprotic Acid Equilibrium
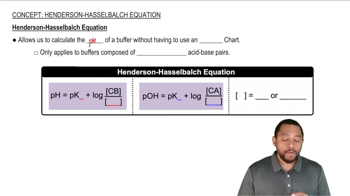
Henderson-Hasselbalch Equation
The Henderson-Hasselbalch equation is a mathematical formula used to relate the pH of a solution to the pKa of the acid and the ratio of the concentrations of the conjugate base to the acid. It is expressed as pH = pKa + log([A-]/[HA]). This equation is essential for calculating the molarity of NaN3 in this problem, as it allows us to determine the relationship between the pH, the concentration of HN3, and the concentration of NaN3.
Recommended video:
Guided course
02:40Henderson-Hasselbalch Equation
Dissociation Constant (Ka)
The dissociation constant (Ka) quantifies the strength of an acid in solution, indicating how well it donates protons (H+) to water. A lower Ka value, such as 1.9 x 10^-5 for HN3, signifies that the acid is weak and does not dissociate completely. Understanding Ka is crucial for calculating pKa and subsequently applying the Henderson-Hasselbalch equation to find the molarity of the conjugate base, NaN3.
Recommended video:
Guided course
03:50Characteristics of Ka and Kb