Consider the gas-phase decomposition of NOBr: 2 NOBr(g) ⇌ 2 NO(g) + Br2(g). (a) When 0.0200 mol of NOBr is added to an empty 1.00-L flask and the decomposition reaction is allowed to reach equilibrium at 300 K, the total pressure in the flask is 0.588 atm. What is the equilibrium constant Kc for this reaction at 300 K? (b) What is the value of Kp for this reaction at 300 K?

Verified step by step guidance

Step 1: Write the balanced chemical equation for the decomposition of NOBr: 2 NOBr(g) ⇌ 2 NO(g) + Br2(g).

Step 2: Define the initial concentration of NOBr. Since 0.0200 mol of NOBr is added to a 1.00-L flask, the initial concentration [NOBr]_0 is 0.0200 M.

Step 3: Use the ideal gas law to relate the total pressure to the concentrations of the gases at equilibrium. The total pressure is given as 0.588 atm, and the reaction involves a change in the number of moles of gas, so consider the stoichiometry of the reaction to express the equilibrium concentrations in terms of a single variable, x, which represents the change in concentration of NOBr.

Step 4: Set up the expression for the equilibrium constant Kc using the equilibrium concentrations. Kc = ([NO]^2[Br2]) / ([NOBr]^2). Substitute the expressions for the equilibrium concentrations in terms of x into this equation.

Step 5: To find Kp, use the relationship between Kc and Kp: Kp = Kc(RT)^(Δn), where Δn is the change in moles of gas (products - reactants), R is the ideal gas constant (0.0821 L·atm/mol·K), and T is the temperature in Kelvin (300 K). Calculate Δn and substitute the values into the equation to find Kp.

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Equilibrium Constant (Kc)

The equilibrium constant, Kc, is a numerical value that expresses the ratio of the concentrations of products to reactants at equilibrium for a given reaction at a specific temperature. It is calculated using the formula Kc = [NO]^2[Br2] / [NOBr]^2, where the brackets denote molarity. A larger Kc indicates a greater concentration of products at equilibrium, while a smaller Kc suggests that reactants are favored.

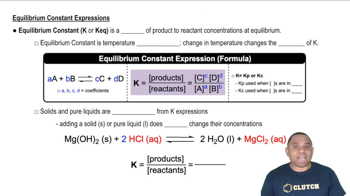
Partial Pressure and Kp

Kp is the equilibrium constant expressed in terms of partial pressures of gases. It is related to Kc through the equation Kp = Kc(RT)^(Δn), where R is the ideal gas constant, T is the temperature in Kelvin, and Δn is the change in moles of gas between products and reactants. For the given reaction, Δn is calculated as the difference in moles of gaseous products and reactants, which is essential for converting Kc to Kp.

Ideal Gas Law

The Ideal Gas Law, represented as PV = nRT, relates the pressure (P), volume (V), number of moles (n), and temperature (T) of an ideal gas. In this context, it helps determine the total pressure in the flask after the decomposition of NOBr. By knowing the number of moles and the volume, one can calculate the pressure, which is crucial for finding the equilibrium concentrations needed to compute Kc.

Recommended video:

Guided course

01:15

Ideal Gas Law Formula

Related Practice

Textbook Question

Refining petroleum involves cracking large hydrocarbon molecules into smaller, more volatile pieces. A simple example of hydrocarbon cracking is the gas-phase thermal decomposition of butane to give ethane and ethylene: (c) A sample of butane having a pressure of 50 atm is heated at 500 °C in a closed container at constant volume. When equilibrium is reached, what percentage of the butane has been converted to ethane and ethylene? What is the total pressure at equilibrium?

views

Textbook Question

At 1000 K, Kp = 2.1 * 106 and ΔH° = - 107.7 kJ for the reaction H21g2 + Br21g2 ∆ 2 HBr1g2.(b) For the equilibrium in part (a), each of the following changes will increase the equilibrium partial pressure of HBr. Choose the change that will cause the greatest increase in the pressure of HBr, and explain your choice.(ii) Adding 0.10 mol of Br2

Textbook Question

Halogen lamps are ordinary tungsten filament lamps in which the lamp bulb contains a small amount of a halogen (often bromine). At the high temperatures of the lamp, the halogens dissociate and exist as single atoms.(c) When the WBr41g2 diffuses back toward the filament, it decomposes, depositing tungsten back onto the fila- ment. Show quantitatively that the pressure of WBr4 from part (a) will cause the reaction in part (a) to go in reverse direction at 2800 K. [The pressure of Br1g2 is still 0.010 atm.] Thus, tungsten is continually recycled from the walls of the bulb back to the filament, allow-ing the bulb to last longer and burn brighter.

Textbook Question

The F-F bond in F₂ is relatively weak because the lone pairs of electrons on one F atom repel the lone pairs on the other F atom; K_p = 7.83 at 1500 K for the reaction F₂(g) ⇌ 2 F(g). (a) If the equilibrium partial pressure of F₂ molecules at 1500 K is 0.200 atm, what is the equilibrium partial pressure of F atoms in atm?

Textbook Question

The F-F bond in F₂ is relatively weak because the lone pairs of electrons on one F atom repel the lone pairs on the other F atom; K_p = 7.83 at 1500 K for the reaction F₂(g) ⇌ 2 F(g). (b) What fraction of the F₂ molecules dissociate at 1500 K?