What is the mole fraction of each component in the liquid mixture in Problem 13.111, and what is the mole fraction of each component in the vapor at 25 °C?

Verified step by step guidance

Step 1: Identify the components of the liquid mixture from Problem 13.111. Let's assume the components are A and B.

Step 2: Determine the number of moles of each component in the liquid mixture. This information should be provided in Problem 13.111.

Step 3: Calculate the mole fraction of each component in the liquid mixture using the formula: \( X_i = \frac{n_i}{n_{\text{total}}} \), where \( n_i \) is the number of moles of component \( i \) and \( n_{\text{total}} \) is the total number of moles in the mixture.

Step 4: Use Raoult's Law to find the partial pressure of each component in the vapor phase: \( P_i = X_i \cdot P_i^0 \), where \( P_i^0 \) is the vapor pressure of pure component \( i \) at 25 °C.

Step 5: Calculate the mole fraction of each component in the vapor phase using the formula: \( Y_i = \frac{P_i}{P_{\text{total}}} \), where \( P_{\text{total}} \) is the sum of the partial pressures of all components.

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

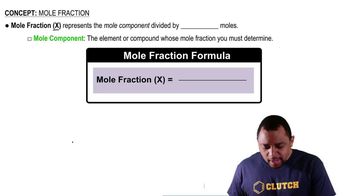
Mole Fraction

Mole fraction is a way of expressing the concentration of a component in a mixture. It is defined as the ratio of the number of moles of a specific component to the total number of moles of all components in the mixture. This dimensionless quantity is useful in calculations involving gas laws and colligative properties, as it provides a clear representation of the relative amounts of substances present.

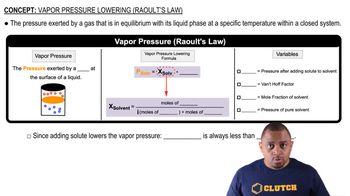
Raoult's Law

Raoult's Law states that the partial vapor pressure of each component in a liquid mixture is equal to the vapor pressure of the pure component multiplied by its mole fraction in the liquid phase. This law is fundamental in understanding how mixtures behave during phase changes, such as evaporation, and is essential for calculating the vapor composition from the liquid composition.

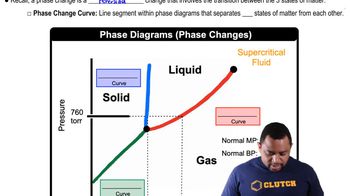
Phase Equilibrium

Phase equilibrium refers to the state in which the rates of the forward and reverse processes of a phase change are equal, resulting in no net change in the amounts of each phase. In the context of mixtures, this concept is crucial for understanding how the composition of a liquid phase relates to that of the vapor phase at a given temperature, particularly when applying Raoult's Law to determine mole fractions in both phases.

Recommended video:

Guided course

03:22

Phase Changes in Diagrams

Related Practice

Textbook Question

Cyclopentane 1C5H102 and cyclohexane 1C6H122 are vola- tile, nonpolar hydrocarbons. At 30.0 °C, the vapor pres- sure of cyclopentane is 385 mm Hg, and the vapor pressure of cyclohexane is 122 mm Hg. What is Xpentane in a mixture of C5H10 and C6H12 that has a vapor pressure of 212 mm Hg at 30.0 °C?

Textbook Question

A solution prepared by dissolving 5.00 g of aspirin, C9H8O4, in 215 g of chloroform has a normal boiling point that is elevated by ΔT = 0.47 °C over that of pure chloro- form. What is the value of the molal boiling-point-elevation constant for chloroform?

Textbook Question

A solution prepared by dissolving 3.00 g of ascorbic acid (vitamin C, C6H8O6) in 50.0 g of acetic acid has a freez- ing point that is depressed by ΔT = 1.33 °C below that ofpure acetic acid. What is the value of the molal freezing- point-depression constant for acetic acid?

Textbook Question

A solution of citric acid, C6H8O7, in 50.0 g of acetic acid has a boiling point elevation of ΔT = 1.76 °C. What is the molality of the solution if the molal boilin# g-point-elevation constant for acetic acid is Kb = 3.07 1°C kg2>mol.