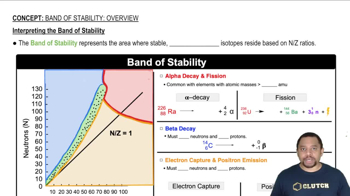
Textbook Question
Examine diagrams for the electron population of the composite s–d band for three metals in question 6. Which metal has the highest melting point? (LO 12.7) (a) Metal 1 (b) Metal 2 (c) Metal 3

 Verified step by step guidance
Verified step by step guidance

Identify each of the following kinds of packing: (b)
Identify each of the following kinds of packing: (d)