A mixture of Ar and N2 gases has a density of 1.413 g/L at STP. What is the mole fraction of each gas?

Verified step by step guidance

Step 1: Recall that at STP (Standard Temperature and Pressure), the molar volume of an ideal gas is 22.414 L/mol. This means that 1 mole of any ideal gas occupies 22.414 liters at STP.

Step 2: Use the formula for density, which is density = mass/volume. Here, the density of the gas mixture is given as 1.413 g/L. We can use this to find the molar mass of the gas mixture by multiplying the density by the molar volume: Molar mass = density * molar volume.

Step 3: Let x be the mole fraction of Ar and (1-x) be the mole fraction of N2. The molar mass of Ar is 39.95 g/mol and the molar mass of N2 is 28.02 g/mol. The molar mass of the mixture can be expressed as: Molar mass of mixture = x * (molar mass of Ar) + (1-x) * (molar mass of N2).

Step 4: Set the expression for the molar mass of the mixture equal to the value calculated in Step 2. This will give you an equation in terms of x, the mole fraction of Ar.

Step 5: Solve the equation from Step 4 for x to find the mole fraction of Ar. The mole fraction of N2 will be 1-x.

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Density and Molar Mass

Density is defined as mass per unit volume and is a crucial property for gases. At standard temperature and pressure (STP), the molar mass of a gas can be related to its density using the ideal gas law. For a mixture, the average molar mass can be calculated from the densities and mole fractions of the individual gases.

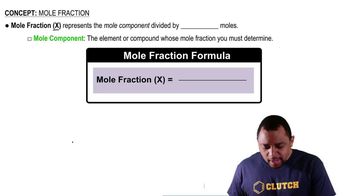
Mole Fraction

Mole fraction is a way of expressing the concentration of a component in a mixture. It is defined as the ratio of the number of moles of a specific component to the total number of moles of all components in the mixture. This concept is essential for determining the composition of gas mixtures and can be calculated once the moles of each gas are known.

Ideal Gas Law

The ideal gas law relates the pressure, volume, temperature, and number of moles of a gas through the equation PV = nRT. This law is fundamental in calculating the behavior of gases under various conditions. For mixtures, the law can be applied to find the total pressure and relate it to the partial pressures of the individual gases, which are directly linked to their mole fractions.

Recommended video:

Guided course

01:15

Ideal Gas Law Formula

Related Practice

Textbook Question

A special gas mixture used in bacterial growth chambers contains 1.00% by weight CO2 and 99.0% O2. What is the partial pressure in atmospheres of each gas at a total pressure of 0.977 atm?

Textbook Question

What is the mole fraction of each gas in the mixture described in Problem 10.83?

Textbook Question

A mixture of 14.2 g of H₂ and 36.7 g of Ar is placed in a 100.0-L container at 290 K. (a) What is the partial pressure of H₂ in atmospheres?

Textbook Question

A mixture of 14.2 g of H₂ and 36.7 g of Ar is placed in a 100.0-L container at 290 K. (b) What is the partial pressure of Ar in atmospheres?

Textbook Question

A 20.0-L flask contains 0.776 g of He and 3.61 g of CO2 at300 K.(a) What is the partial pressure of He in mm Hg?