The wavenumber l is the number of waves that exist over a specified distance, very often 1 cm. The wavenumber can easily be calculated by taking the reciprocal of the wavelength. Give typical wavenumbers for (a) X-rays (λ = 1 nm) (b) visible light (λ = 500 nm) (c) microwaves (λ = 1 mm).

Verified step by step guidance

Step 1: Understand the relationship between wavenumber and wavelength. The wavenumber (\( \tilde{\nu} \)) is defined as the reciprocal of the wavelength (\( \lambda \)), expressed as \( \tilde{\nu} = \frac{1}{\lambda} \).

Step 2: Convert the given wavelengths into centimeters, as wavenumbers are typically expressed in cm\(^{-1}\). Remember that 1 nm = 1 \times 10^{-7} cm and 1 mm = 0.1 cm.

Step 3: Calculate the wavenumber for X-rays. Given \( \lambda = 1 \text{ nm} \), convert this to cm and then find the wavenumber using the formula \( \tilde{\nu} = \frac{1}{\lambda} \).

Step 4: Calculate the wavenumber for visible light. Given \( \lambda = 500 \text{ nm} \), convert this to cm and then find the wavenumber using the formula \( \tilde{\nu} = \frac{1}{\lambda} \).

Step 5: Calculate the wavenumber for microwaves. Given \( \lambda = 1 \text{ mm} \), convert this to cm and then find the wavenumber using the formula \( \tilde{\nu} = \frac{1}{\lambda} \).

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Wavenumber

Wavenumber is a measure of the number of waves in a given distance, typically expressed in reciprocal centimeters (cm⁻¹). It is calculated as the reciprocal of the wavelength, which means that shorter wavelengths correspond to higher wavenumbers. This concept is crucial for understanding the behavior of electromagnetic radiation across different regions of the spectrum.

Wavelength

Wavelength is the distance between successive peaks of a wave, commonly measured in meters, nanometers, or millimeters. It is inversely related to frequency and directly affects the energy of the electromagnetic radiation. Understanding wavelength is essential for calculating wavenumber and for distinguishing between different types of electromagnetic radiation, such as X-rays, visible light, and microwaves.

Electromagnetic Spectrum

The electromagnetic spectrum encompasses all types of electromagnetic radiation, ranging from gamma rays and X-rays to visible light and radio waves. Each type of radiation has a specific range of wavelengths and corresponding energies. Familiarity with the electromagnetic spectrum is important for contextualizing the wavenumbers of different types of radiation, as it helps to categorize their properties and applications in various fields.

Recommended video:

Guided course

02:53

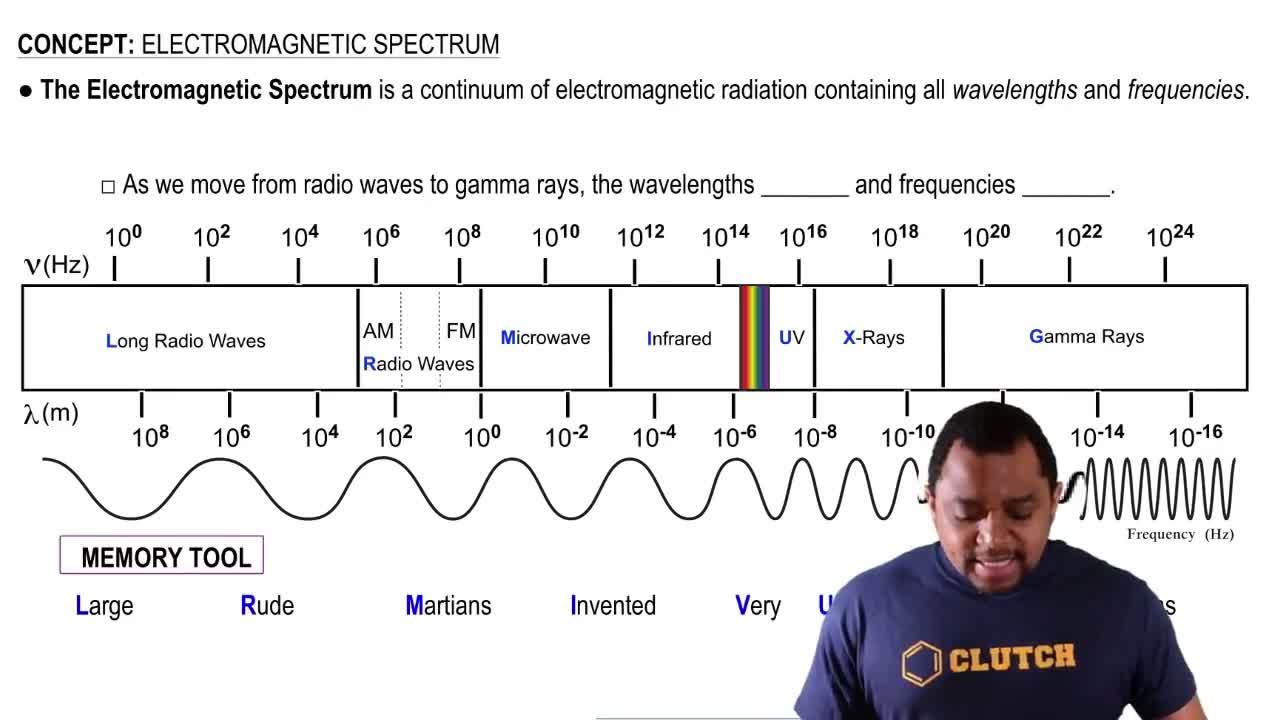
Electromagnetic Spectrum

Related Practice

Textbook Question

Four possible electron configurations for a carbon atom are shown below, but only one schematic represents the correct configuration for a carbon atom in its ground state. Which one is the correct electron configuration?

Textbook Question

Four possible electron configurations for a nitrogen atom are shown below, but only one schematic represents the correct configuration for a nitrogen atom in its ground state. Which configurations violate the Pauli exclusion principle?

views

rank

Textbook Question

State where in the periodic table these elements appear: (a) elements with the valence-shell electron configuration ns2np5 (b) elements that have three unpaired p electrons (c) an element whose valence electrons are 4s24p1 (d) the d-block elements [Section 6.9]

Textbook Question

Label each of the following statements as true or false. a. Visible light is a form of electromagnetic radiation.

Textbook Question

Label each of the following statements as true or false. b. Ultraviolet light has longer wavelengths than visible light.