The speed of sound in dry air at is 343 m/s, and the middle C on a piano keyboard has a frequency of 261 Hz. a. What is the wavelength of the sound wave corresponding to a middle C?
Ch.6 - Electronic Structure of Atoms

Brown15th EditionChemistry: The Central ScienceISBN: 9780137542970Not the one you use?Change textbook
Chapter 6, Problem 1b
The speed of sound in dry air at is 343 m/s, and the middle C on a piano keyboard has a frequency of 261 Hz. b. What would be the frequency of electromagnetic radiation with the same wavelength?
 Verified step by step guidance
Verified step by step guidance1
Identify the relationship between speed, frequency, and wavelength for sound waves: \( v = f \cdot \lambda \), where \( v \) is the speed of sound, \( f \) is the frequency, and \( \lambda \) is the wavelength.
Calculate the wavelength of the sound wave using the given speed of sound (343 m/s) and the frequency of middle C (261 Hz): \( \lambda = \frac{v}{f} \).
Recognize that electromagnetic radiation also follows the wave equation: \( c = f_{em} \cdot \lambda \), where \( c \) is the speed of light (approximately \( 3.00 \times 10^8 \) m/s), \( f_{em} \) is the frequency of the electromagnetic wave, and \( \lambda \) is the wavelength.
Use the wavelength calculated from the sound wave to find the frequency of the electromagnetic radiation: \( f_{em} = \frac{c}{\lambda} \).
Substitute the known values into the equation to solve for the frequency of the electromagnetic radiation.

Verified video answer for a similar problem:
This video solution was recommended by our tutors as helpful for the problem above.
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Wave Speed
Wave speed is the distance traveled by a wave per unit time. In the context of sound, it is determined by the medium through which it travels, such as air. The speed of sound in dry air at room temperature is approximately 343 m/s, which is essential for calculating the wavelength of sound waves.
Recommended video:
Guided course

Speed of Light Formula
Frequency and Wavelength Relationship
The relationship between frequency (f) and wavelength (λ) of a wave is described by the equation v = fλ, where v is the wave speed. This means that the frequency of a wave is inversely proportional to its wavelength; as frequency increases, wavelength decreases, and vice versa. This principle applies to both sound and electromagnetic waves.
Recommended video:
Guided course
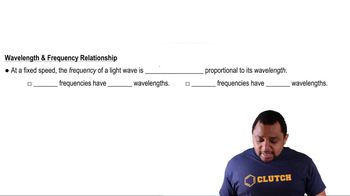
Frequency-Wavelength Relationship
Electromagnetic Radiation
Electromagnetic radiation encompasses a range of waves, including visible light, radio waves, and X-rays, all of which travel at the speed of light in a vacuum (approximately 3 x 10^8 m/s). The frequency of electromagnetic radiation can be calculated using the same wave speed and wavelength relationship as sound, allowing for comparisons between different types of waves.
Recommended video:
Guided course
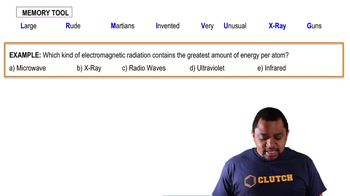
Electromagnetic Radiation Example
Related Practice
Textbook Question
Textbook Question
A popular kitchen appliance produces electromagnetic radiation with a frequency of 2450 MHz. With reference to Figure 6.4, answer the following: (a) Estimate the wavelength of this radiation.
4
views
1
rank
Textbook Question
A popular kitchen appliance produces electromagnetic radiation with a frequency of 2450 MHz. With reference to Figure 6.4, answer the following: (b) Would the radiation produced by the appliance be visible to the human eye?
5
views
Textbook Question
A popular kitchen appliance produces electromagnetic radiation with a frequency of 2450 MHz. With reference to Figure 6.4, answer the following: (c) If the radiation is not visible, do photons of this radiation have more or less energy than photons of visible light?
5
views
