A popular kitchen appliance produces electromagnetic radiation with a frequency of 2450 MHz. With reference to Figure 6.4, answer the following: (a) Estimate the wavelength of this radiation.

Verified step by step guidance

Convert the frequency from MHz to Hz for easier calculation. Remember that 1 MHz equals 1,000,000 Hz, so multiply the given frequency by 1,000,000.

Use the speed of light equation, which is c = \lambda \nu, where c is the speed of light (approximately 3.00 \times 10^8 m/s), \lambda is the wavelength, and \nu is the frequency. Rearrange the equation to solve for the wavelength (\lambda).

Substitute the frequency value in Hz and the speed of light into the rearranged equation \lambda = \frac{c}{\nu}.

Calculate the wavelength by dividing the speed of light by the frequency. Ensure your units are consistent (meters for wavelength and Hz for frequency).

Express the final wavelength in meters, which is the standard unit for wavelength in the context of electromagnetic radiation.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.

Video duration:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Electromagnetic Radiation

Electromagnetic radiation encompasses a range of waves, including radio waves, microwaves, and visible light, characterized by their frequency and wavelength. The frequency, measured in hertz (Hz), indicates how many cycles of the wave occur per second, while the wavelength, measured in meters, is the distance between successive peaks of the wave. Understanding this relationship is crucial for estimating wavelength from frequency.

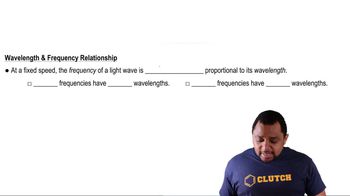
Wavelength and Frequency Relationship

The relationship between wavelength (λ) and frequency (f) of electromagnetic radiation is described by the equation c = λf, where c is the speed of light (approximately 3.00 x 10^8 m/s). This equation allows us to calculate the wavelength when the frequency is known, and vice versa. In this case, knowing the frequency of 2450 MHz enables us to determine the corresponding wavelength.

Unit Conversion

In scientific calculations, unit conversion is often necessary to ensure consistency in measurements. For instance, the frequency given in megahertz (MHz) must be converted to hertz (Hz) for use in the wavelength formula. Since 1 MHz equals 10^6 Hz, converting 2450 MHz to Hz is essential for accurately calculating the wavelength of the electromagnetic radiation produced by the kitchen appliance.

Recommended video:

Guided course

01:56

Conversion Factors

Related Practice

Textbook Question

The speed of sound in dry air at is 343 m/s, and the middle C on a piano keyboard has a frequency of 261 Hz. a. What is the wavelength of the sound wave corresponding to a middle C?

Textbook Question

The speed of sound in dry air at is 343 m/s, and the middle C on a piano keyboard has a frequency of 261 Hz. b. What would be the frequency of electromagnetic radiation with the same wavelength?

Textbook Question

A popular kitchen appliance produces electromagnetic radiation with a frequency of 2450 MHz. With reference to Figure 6.4, answer the following: (b) Would the radiation produced by the appliance be visible to the human eye?

views

Textbook Question

A popular kitchen appliance produces electromagnetic radiation with a frequency of 2450 MHz. With reference to Figure 6.4, answer the following: (c) If the radiation is not visible, do photons of this radiation have more or less energy than photons of visible light?

views

Textbook Question

A popular kitchen appliance produces electromagnetic radiation with a frequency of 2450 MHz. With reference to Figure 6.4, answer the following: (d) Which of the following is the appliance likely to be? (i) A toaster oven, (ii) A microwave oven, or (iii) An electric hotplate.

views