Skip to main content
Pearson+ LogoPearson+ Logo
Ch.21 - Nuclear Chemistry
All textbooksBrown 15th EditionCh.21 - Nuclear ChemistryProblem 42
Chapter 21, Problem 42

A wooden artifact from a Chinese temple has a 14C activity of 38.0 counts per minute as compared with an activity of 58.2 counts per minute for a standard of zero age. From the half-life for 14C decay, 5715 years, determine the age of the artifact.

Verified step by step guidance
1
Step 1: Understand the concept of radioactive decay and the use of carbon-14 dating. Carbon-14 dating is used to determine the age of an artifact by comparing its current 14C activity to that of a standard of zero age.
Step 2: Use the formula for radioactive decay: \( N(t) = N_0 e^{-\lambda t} \), where \( N(t) \) is the current activity, \( N_0 \) is the initial activity, \( \lambda \) is the decay constant, and \( t \) is the time elapsed.
Step 3: Calculate the decay constant \( \lambda \) using the half-life formula: \( \lambda = \frac{\ln(2)}{\text{half-life}} \). Substitute the given half-life of 5715 years into the formula.
Step 4: Rearrange the decay formula to solve for \( t \): \( t = \frac{1}{\lambda} \ln\left(\frac{N_0}{N(t)}\right) \). Substitute the given activities (38.0 counts per minute for the artifact and 58.2 counts per minute for the standard) into the equation.
Step 5: Calculate \( t \) to find the age of the artifact. This will give you the time elapsed since the artifact had the same 14C activity as the standard of zero age.

Key Concepts

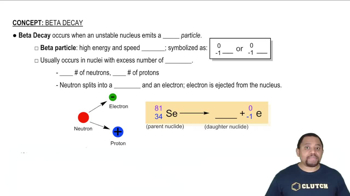
Here are the essential concepts you must grasp in order to answer the question correctly.

Radiocarbon Dating

Radiocarbon dating is a method used to determine the age of organic materials by measuring the amount of carbon-14 (14C) remaining in a sample. 14C is a radioactive isotope of carbon that is formed in the atmosphere and taken up by living organisms. When an organism dies, it stops absorbing 14C, and the isotope begins to decay at a known rate, characterized by its half-life.

Half-Life

The half-life of a radioactive isotope is the time required for half of the isotope in a sample to decay. For 14C, the half-life is approximately 5715 years. This concept is crucial for calculating the age of an artifact, as it allows us to determine how many half-lives have passed since the organism's death based on the remaining activity of 14C in the sample.
Recommended video:
Guided course
02:17
Zero-Order Half-life

Exponential Decay

Exponential decay describes the process by which a quantity decreases at a rate proportional to its current value. In the context of radioactive decay, the activity of a radioactive substance decreases exponentially over time. The relationship can be expressed mathematically, allowing for the calculation of the age of an artifact by comparing its current activity to that of a standard reference.
Recommended video:
Guided course
03:01
Beta Decay
Related Practice
Textbook Question

The cloth shroud from around a mummy is found to have a 14C activity of 9.7 disintegrations per minute per gram of carbon as compared with living organisms that undergo 16.3 disintegrations per minute per gram of carbon. From the half-life for 14C decay, 5730 yr, calculate the age of the shroud.

Textbook Question

Potassium-40 decays to argon-40 with a half-life of 1.27 * 109 yr. What is the age of a rock in which the mass ratio of 40Ar to 40K is 4.2?