Textbook Question
A voltaic cell utilizes the following reaction: Al1s2 + 3 Ag+1aq2 ¡ Al3+1aq2 + 3 Ag1s2 What is the effect on the cell emf of each of the following changes? (a) Water is added to the anode half-cell, diluting the solution.
Ch.20 - Electrochemistry
Chapter 20, Problem 70
A voltaic cell utilizes the following reaction and operates at 298 K: 3 Ce⁴⁺(aq) + Cr(s) → 3 Ce³⁺(aq) + Cr³⁺(aq) (b) What is the emf of this cell when [Ce⁴⁺] = 3.0 M, [Ce³⁺] = 0.10 M, and [Cr³⁺] = 0.010 M? (c) What is the emf of the cell when [Ce⁴⁺] = 0.010 M, [Ce³⁺] = 2.0 M, and [Cr³⁺] = 1.5 M?
Verified step by step guidance1
Step 1: Identify the half-reactions and their standard reduction potentials. The given reaction is 3 Ce⁴⁺(aq) + Cr(s) → 3 Ce³⁺(aq) + Cr³⁺(aq). The half-reactions are: Ce⁴⁺ + e⁻ → Ce³⁺ and Cr → Cr³⁺ + 3e⁻. Look up the standard reduction potentials (E°) for these half-reactions in a standard reduction potential table.
Step 2: Calculate the standard cell potential (E°cell). Use the formula E°cell = E°cathode - E°anode. The cathode is where reduction occurs (Ce⁴⁺ to Ce³⁺), and the anode is where oxidation occurs (Cr to Cr³⁺). Substitute the standard reduction potentials into the formula to find E°cell.
Step 3: Use the Nernst equation to calculate the cell potential (Ecell) under non-standard conditions. The Nernst equation is Ecell = E°cell - (RT/nF) * ln(Q), where R is the gas constant (8.314 J/mol·K), T is the temperature in Kelvin (298 K), n is the number of moles of electrons transferred (3 in this case), F is Faraday's constant (96485 C/mol), and Q is the reaction quotient.
Step 4: Calculate the reaction quotient (Q) for the given concentrations. For the reaction 3 Ce⁴⁺(aq) + Cr(s) → 3 Ce³⁺(aq) + Cr³⁺(aq), Q = ([Ce³⁺]^3 * [Cr³⁺]) / [Ce⁴⁺]^3. Substitute the given concentrations into this expression to find Q for each scenario.
Step 5: Substitute the values of E°cell, R, T, n, F, and Q into the Nernst equation to calculate the emf of the cell for each set of conditions. This will give you the emf for both scenarios: (b) [Ce⁴⁺] = 3.0 M, [Ce³⁺] = 0.10 M, [Cr³⁺] = 0.010 M and (c) [Ce⁴⁺] = 0.010 M, [Ce³⁺] = 2.0 M, [Cr³⁺] = 1.5 M.
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Electrochemical Cells
Electrochemical cells, such as voltaic cells, convert chemical energy into electrical energy through redox reactions. In a voltaic cell, oxidation occurs at the anode and reduction at the cathode, generating a flow of electrons that can be harnessed for electrical work. Understanding the components and functioning of these cells is crucial for calculating their electromotive force (emf).
Recommended video:
Guided course
02:46
Electrochemical Cells
Nernst Equation
The Nernst equation relates the emf of an electrochemical cell to the concentrations of the reactants and products involved in the redox reaction. It allows for the calculation of the cell potential under non-standard conditions by incorporating the reaction quotient, Q, which reflects the current concentrations of the species. This equation is essential for determining how changes in concentration affect the cell's emf.
Recommended video:
Guided course
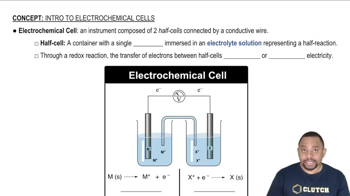
01:17The Nernst Equation
Standard Electrode Potentials
Standard electrode potentials are measured values that indicate the tendency of a species to be reduced, measured under standard conditions (1 M concentration, 1 atm pressure, and 25°C). These values are used to calculate the standard emf of a cell and are critical for understanding the driving force behind the redox reactions in the cell. The difference in standard potentials between the cathode and anode determines the overall cell potential.
Recommended video:
Guided course
01:27Standard Cell Potential
Related Practice
Textbook Question
A voltaic cell is constructed that uses the following reaction and operates at 298 K: Zn(s) + Ni2+(aq) → Zn2+(aq) + Ni(s) (b) What is the emf of this cell when [Ni2+] = 3.00 M and [Zn2+] = 0.100 M? (c) What is the emf of the cell when [Ni2+] = 0.200 M and [Zn2+] = 0.900 M?
Textbook Question
A voltaic cell utilizes the following reaction: 4 Fe2+1aq2 + O21g2 + 4 H+1aq2 ¡ 4 Fe3+1aq2 + 2 H2O1l2 (a) What is the emf of this cell under standard conditions?
Textbook Question
A voltaic cell utilizes the following reaction: 4 Fe2+1aq2 + O21g2 + 4 H+1aq2 ¡ 4 Fe3+1aq2 + 2 H2O1l2 (b) What is the emf of this cell when 3Fe2+4 = 1.3 M, 3Fe3+4= 0.010 M, PO2 = 0.50 atm, and the pH of the solution in the cathode half-cell is 3.50?
Textbook Question
A voltaic cell utilizes the following reaction: 2 Fe3+1aq2 + H21g2 ¡ 2 Fe2+1aq2 + 2 H+1aq2 (a) What is the emf of this cell under standard conditions?