Textbook Question
(a) Does the entropy of the surroundings increase for spontaneous processes?

 Verified step by step guidance
Verified step by step guidance
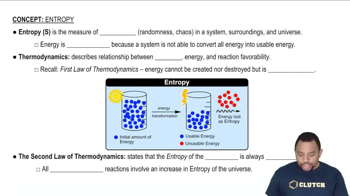


(a) Does the entropy of the surroundings increase for spontaneous processes?
(b) In a particular spontaneous process the entropy of the system decreases. What can you conclude about the sign and magnitude of ΔSsurr?
(c) During a certain reversible process, the surroundings undergo an entropy change, ΔSsurr = -78 J/K. What is the entropy change of the system for this process?
For the isothermal expansion of a gas into a vacuum, ΔE = 0, q = 0, and w = 0. (b) Explain why no work is done by the system during this process.
(a) What is the difference between a state and a microstate of a system?
(b) As a system goes from state A to state B, its entropy decreases. What can you say about the number of microstates corresponding to each state?