The element gallium (Ga) freezes at 29.8 °C, and its molar enthalpy of fusion is ΔHfus = 5.59 kJ/mol. (a) When molten gallium solidifies to Ga(s) at its normal melting point, is ΔS positive or negative?

(a) Does the entropy of the surroundings increase for spontaneous processes?
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
Entropy
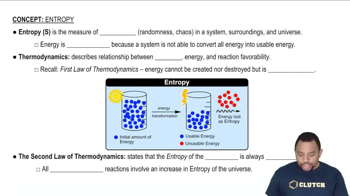
Spontaneous Processes

Second Law of Thermodynamics

The element gallium (Ga) freezes at 29.8 °C, and its molar enthalpy of fusion is ΔHfus = 5.59 kJ/mol. (b) Calculate the value of ΔS when 60.0 g of Ga(l) solidifies at 29.8 °C.
Indicate whether each statement is true or false. (c) In a certain spontaneous process the system undergoes an entropy change of 4.2 J/K; therefore, the entropy change of the surroundings must be -4.2 J/K.
(b) In a particular spontaneous process the entropy of the system decreases. What can you conclude about the sign and magnitude of ΔSsurr?
(c) During a certain reversible process, the surroundings undergo an entropy change, ΔSsurr = -78 J/K. What is the entropy change of the system for this process?
(a) What sign for Δ𝑆 do you expect when the pressure on 0.600 mol of an ideal gas at 350 K is increased isothermally from an initial pressure of 0.750 atm?
(b) If the final pressure on the gas is 1.20 atm, calculate the entropy change for the process.
(c) Which of the following statements about this process are true? (i) The entropy change you calculated will be the same for at any other constant temperature. (ii) The value of Δ𝑆 you calculated is valid only if the compression is done irreversibly. (iii) If the number of moles of gas being compressed were decreased by a factor of three, the entropy change would increase by a factor of three.
