Textbook Question
The maximum allowable concentration of lead in drinking water is 9.0 ppb. (a) Calculate the molarity of lead in a 9.0-ppb solution.
Ch.13 - Properties of Solutions
Chapter 13, Problem 101a
Acetonitrile (CH3CN) is a polar organic solvent that dissolves a wide range of solutes, including many salts. The density of a 1.80 M LiBr solution in acetonitrile is 0.826 g/cm3. Calculate the concentration of the solution in (a) molality,
Verified step by step guidance1
Start by understanding the relationship between molarity and molality. Molarity (M) is moles of solute per liter of solution, while molality (m) is moles of solute per kilogram of solvent.
Calculate the mass of the solution using its density. Use the formula: \( \text{mass of solution} = \text{density} \times \text{volume} \). Assume 1 L of solution for simplicity, so the mass of the solution is \( 0.826 \text{ g/cm}^3 \times 1000 \text{ cm}^3 \).
Determine the moles of LiBr in the solution. Since the solution is 1.80 M, there are 1.80 moles of LiBr in 1 L of solution.
Calculate the mass of LiBr using its molar mass. The molar mass of LiBr is approximately 86.85 g/mol, so the mass of LiBr is \( 1.80 \text{ moles} \times 86.85 \text{ g/mol} \).
Find the mass of the solvent (acetonitrile) by subtracting the mass of LiBr from the total mass of the solution. Finally, calculate the molality using the formula: \( \text{molality} = \frac{\text{moles of solute}}{\text{kilograms of solvent}} \).
Verified video answer for a similar problem:
This video solution was recommended by our tutors as helpful for the problem above.
Video duration:
3mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Molarity
Molarity is a measure of concentration defined as the number of moles of solute per liter of solution. It is commonly used in chemistry to express the concentration of a solution. In this case, the 1.80 M LiBr solution indicates that there are 1.80 moles of lithium bromide dissolved in one liter of acetonitrile.
Recommended video:
Guided course
01:13
Molarity
Molality
Molality is another measure of concentration, defined as the number of moles of solute per kilogram of solvent. Unlike molarity, which depends on the volume of the solution, molality is based on the mass of the solvent, making it useful for temperature-dependent calculations. To convert from molarity to molality, the mass of the solvent must be known.
Recommended video:
Guided course
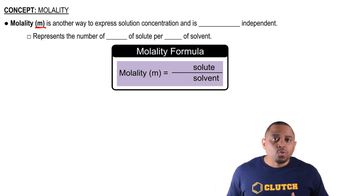
00:40Molality
Density
Density is defined as mass per unit volume and is a critical property in calculating concentrations. In this context, the density of the solution (0.826 g/cm³) allows for the conversion between the mass of the solution and its volume. This information is essential for determining the mass of the solvent when calculating molality from the given molarity.
Recommended video:
Guided course
01:56Density Concepts
Related Practice
Textbook Question
The maximum allowable concentration of lead in drinking water is 9.0 ppb. (b) How many grams of lead are in a swimming pool containing 9.0 ppb lead in 60 m3 of water?
Textbook Question
The first stage of treatment at a reverse osmosis plant is to flow the water through rock, sand, and gravel as shown here. Would this step remove particulate matter? Would this step remove dissolved salts?
Textbook Question
Acetonitrile (CH3CN) is a polar organic solvent that dissolves a wide range of solutes, including many salts. The density of a 1.80 M LiBr solution in acetonitrile is 0.826 g/cm3. Calculate the concentration of the solution in (b) mole fraction of LiBr,
1
views
Textbook Question
Two beakers are placed in a sealed box at 25 °C. One beaker contains 30.0 mL of a 0.050 M aqueous solution of a nonvolatile nonelectrolyte. The other beaker contains 30.0 mL of a 0.035 M aqueous solution of NaCl. The water vapor from the two solutions reaches equilibrium. (a) In which beaker does the solution level rise, and in which one does it fall?
Textbook Question
Two beakers are placed in a sealed box at 25 °C. One beaker contains 30.0 mL of a 0.050 M aqueous solution of a nonvolatile nonelectrolyte. The other beaker contains 30.0 mL of a 0.035 M aqueous solution of NaCl. The water vapor from the two solutions reaches equilibrium. (b) What are the volumes in the two beakers when equilibrium is attained, assuming ideal behavior?