A particular form of cinnabar (HgS) adopts the zinc blende structure. The length of the unit cell edge is 5.852 Å. (a) Calculate the density of HgS in this form. (c) Which of the two substances has the higher density? How do you account for the difference in densities?

Verified step by step guidance

Step 1: Understand the zinc blende structure. In the zinc blende structure, each unit cell contains 4 formula units of the compound. For HgS, this means there are 4 Hg atoms and 4 S atoms per unit cell.

Step 2: Calculate the mass of the unit cell. Use the molar masses of Hg (200.59 g/mol) and S (32.07 g/mol) to find the mass of one formula unit of HgS, then multiply by 4 to find the mass of the unit cell.

Step 3: Calculate the volume of the unit cell. The volume of a cubic unit cell is given by the cube of the edge length. Convert the edge length from Å to cm (1 Å = 1 x 10^-8 cm) and calculate the volume.

Step 4: Calculate the density of HgS. Density is mass divided by volume. Use the mass of the unit cell from Step 2 and the volume from Step 3 to find the density of HgS.

Step 5: Compare the density of HgS with the other substance. If the other substance's density is known, compare it with the calculated density of HgS to determine which is higher. Discuss factors such as atomic mass and packing efficiency that could account for differences in density.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.

Video duration:

Was this helpful?

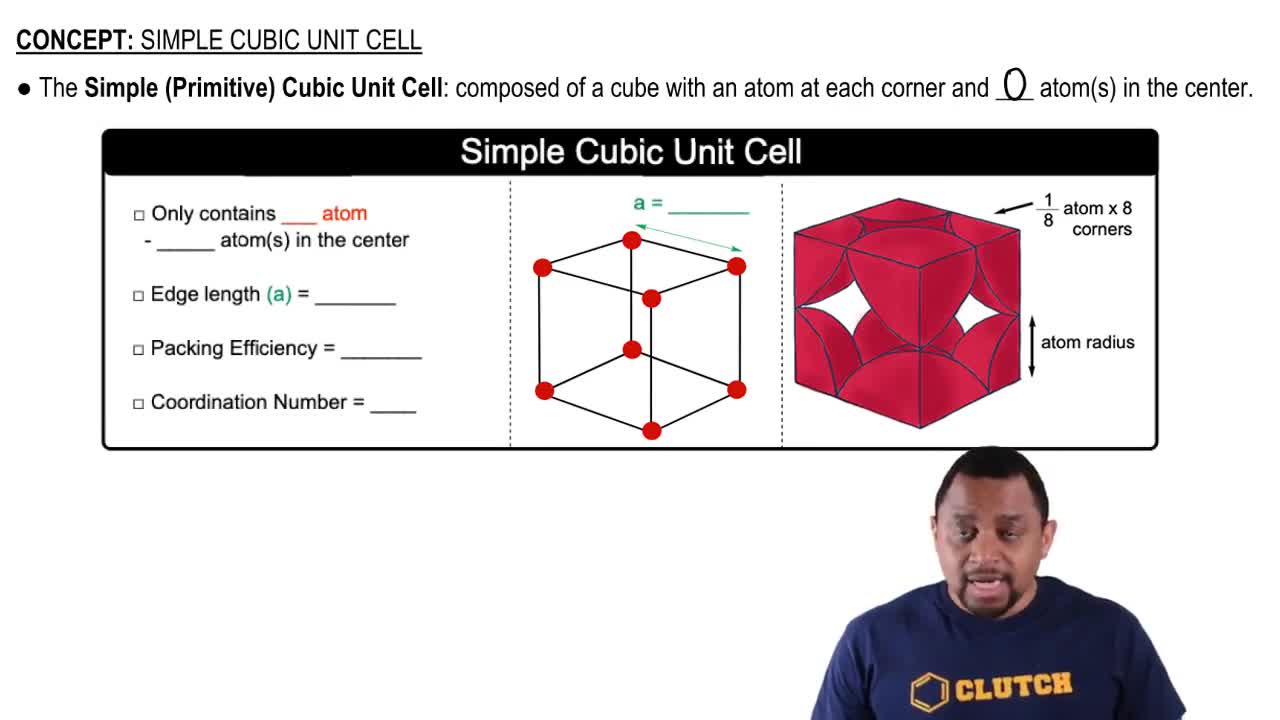
Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Density

Density is defined as mass per unit volume, typically expressed in grams per cubic centimeter (g/cm³). It is a crucial property that helps compare the compactness of different substances. In this context, density can be calculated using the formula: density = mass/volume, where the mass is derived from the molar mass of the substance and the volume is determined by the unit cell dimensions.

Unit Cell and Crystal Structure

A unit cell is the smallest repeating unit in a crystal lattice that reflects the overall symmetry and structure of the crystal. The zinc blende structure, for example, is a face-centered cubic arrangement where each atom is surrounded by four others in a tetrahedral configuration. Understanding the unit cell dimensions, such as the edge length, is essential for calculating the volume of the unit cell, which is necessary for density calculations.

Molar Mass

Molar mass is the mass of one mole of a substance, typically expressed in grams per mole (g/mol). It is a critical factor in determining the mass of the unit cell when calculating density. For the substances in question, knowing the molar masses of cinnabar (HgS) and the other substance allows for a direct comparison of their densities, as the substance with the higher molar mass will generally have a higher density if the volume is similar.

Recommended video:

Guided course

02:11

Molar Mass Concept

Related Practice

Textbook Question

Tausonite, a mineral composed of Sr, O, and Ti, has the cubic unit cell shown in the drawing. (a) What is the empirical formula of this mineral?

Textbook Question

The unit cell of a compound containing Co and O has a unit cell shown in the diagram. The Co atoms are on the corners, and the O atoms are completely within the unit cell. a. What is the empirical formula of this compound? b. What is the oxidation state of the metal?

Textbook Question

A particular form of cinnabar (HgS) adopts the zinc blende structure. The length of the unit cell edge is 5.852 Å. (b) The mineral tiemannite (HgSe) also forms a solid phase with the zinc blende structure. The length of the unit cell edge in this mineral is 6.085 Å. What accounts for the larger unit cell length in tiemmanite?

views

Textbook Question

CuI, CsI, and NaI each adopt a different type of structure. The three different structures to consider are those shown in Figure 12.25 for CsCl, NaCl, and ZnS. a. Use ionic radii, Cs+(𝑟=1.81 Å), Na+(𝑟=1.16 Å), Cu+(𝑟=0.74 Å), and, I−(𝑟=2.06 Å), to predict which compound will crystallize with which structure.