How many unique combinations of the quantum numbers l and ml are there when (a) n = 1 (b) n = 5?

Verified step by step guidance

insert step 1> Determine the possible values of the azimuthal quantum number \( l \) for a given principal quantum number \( n = 5 \). The values of \( l \) range from 0 to \( n-1 \).

insert step 2> List the possible values of \( l \) for \( n = 5 \): \( l = 0, 1, 2, 3, 4 \).

insert step 3> For each value of \( l \), determine the possible values of the magnetic quantum number \( m_l \). The values of \( m_l \) range from \( -l \) to \( +l \).

insert step 4> Calculate the number of \( m_l \) values for each \( l \): \( l = 0 \) has 1 value, \( l = 1 \) has 3 values, \( l = 2 \) has 5 values, \( l = 3 \) has 7 values, and \( l = 4 \) has 9 values.

insert step 5> Add the number of \( m_l \) values for all \( l \) to find the total number of unique combinations of \( l \) and \( m_l \) for \( n = 5 \).

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.

Video duration:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Quantum Numbers

Quantum numbers are sets of numerical values that describe the unique quantum state of an electron in an atom. There are four quantum numbers: principal (n), azimuthal (l), magnetic (ml), and spin (ms). Each quantum number provides specific information about the electron's energy level, shape of the orbital, orientation, and spin direction.

Principal Quantum Number (n)

The principal quantum number (n) indicates the main energy level or shell of an electron in an atom. It can take positive integer values (1, 2, 3, ...), with higher values corresponding to higher energy levels and greater distances from the nucleus. In this case, n = 5 means we are considering the fifth energy level.

Azimuthal Quantum Number (l) and Magnetic Quantum Number (ml)

The azimuthal quantum number (l) defines the shape of the orbital and can take values from 0 to n-1. For n = 5, l can be 0, 1, 2, 3, or 4, corresponding to s, p, d, f, and g orbitals, respectively. The magnetic quantum number (ml) specifies the orientation of the orbital and can take values from -l to +l, resulting in multiple ml values for each l, thus creating unique combinations.

Recommended video:

Guided course

03:06

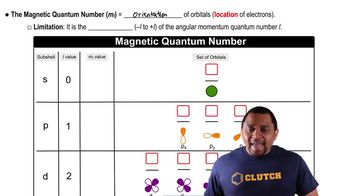
Magnetic Quantum Number

Related Practice

Textbook Question

Using Heisenberg's uncertainty principle, calculate the uncertainty in the position of (b) a proton moving at a speed of 15.00 { 0.012 * 104 m/s. (The mass of a proton is given in the table of fundamental constants in the inside cover of the text.)

Textbook Question

Calculate the uncertainty in the position of (a) an electron moving at a speed of 13.00 ± 0.012 × 10⁵ m/s (b) a neutron moving at this same speed. (The masses of an electron and a neutron are given in the table of fundamental constants in the inside cover of the text.)

Textbook Question

(a) For n = 4, what are the possible values of l?

Textbook Question

Give the numerical values of n and l corresponding to each of the following orbital designations: (a) 3p (b) 2s (c) 4f

Textbook Question

Give the numerical values of n and l corresponding to each of the following orbital designations: (d) 5d.

Textbook Question

Give the values for n, l, and ml for (a) each orbital in the 3p subshell, (b) each orbital in the 4f subshell.