Textbook Question
(a) What is the electrostatic potential energy (in joules) between two electrons that are separated by 62 pm?
Ch.5 - Thermochemistry
Chapter 5, Problem 15
(b) The force of gravity acting between two objects is given by the equation F = G * (m1 * m2) / d^2, where G is the gravitational constant, G = 6.674 * 10^-11 N*m^2/kg^2, m1 and m2 are the masses of the two objects, and d is the distance separating them. What is the gravitational force of attraction (in Newtons) between the electron and proton? (c) How many times larger is the electrostatic force of attraction?
Verified step by step guidance1
Identify the given values: the gravitational constant \( G = 6.674 \times 10^{-11} \text{ N} \cdot \text{m}^2/\text{kg}^2 \), the mass of an electron \( m_e = 9.109 \times 10^{-31} \text{ kg} \), the mass of a proton \( m_p = 1.673 \times 10^{-27} \text{ kg} \), and the typical distance between an electron and a proton in a hydrogen atom, approximately \( d = 5.29 \times 10^{-11} \text{ m} \).
Substitute the known values into the gravitational force equation: \( F = G \cdot \frac{m_1 \cdot m_2}{d^2} \). Here, \( m_1 = m_e \) and \( m_2 = m_p \).
Calculate the gravitational force \( F \) by substituting the values: \( F = 6.674 \times 10^{-11} \cdot \frac{(9.109 \times 10^{-31}) \cdot (1.673 \times 10^{-27})}{(5.29 \times 10^{-11})^2} \).
To find the electrostatic force, use Coulomb's law: \( F_e = k \cdot \frac{|q_1 \cdot q_2|}{d^2} \), where \( k = 8.988 \times 10^9 \text{ N} \cdot \text{m}^2/\text{C}^2 \) is Coulomb's constant, and \( q_1 = q_2 = 1.602 \times 10^{-19} \text{ C} \) are the charges of the electron and proton.
Calculate the electrostatic force \( F_e \) and then determine how many times larger it is than the gravitational force by dividing \( F_e \) by \( F \).
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Gravitational Force
The gravitational force is the attractive force between two masses, described by Newton's law of universal gravitation. It is directly proportional to the product of the masses and inversely proportional to the square of the distance between their centers. In this context, the equation F = G * (m1 * m2) / d^2 quantifies this force, where G is the gravitational constant.
Recommended video:
Guided course
06:44
Types of Intermolecular Forces
Electrostatic Force
The electrostatic force is the force of attraction or repulsion between charged particles, described by Coulomb's law. This force is directly proportional to the product of the magnitudes of the charges and inversely proportional to the square of the distance between them. It is significantly stronger than gravitational force at the atomic level, which is crucial for understanding interactions between subatomic particles like electrons and protons.
Recommended video:
Guided course
01:59Intermolecular vs Intramolecular Forces
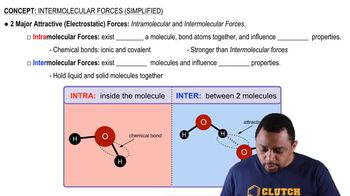
Comparison of Forces
Comparing gravitational and electrostatic forces involves calculating the ratio of the two forces acting between the same pair of particles. This comparison highlights the relative strength of these fundamental forces, illustrating that while gravity is a universal force, electrostatic interactions dominate at the scale of atoms and molecules, influencing chemical bonding and structure.
Recommended video:
Guided course
06:44Types of Intermolecular Forces
Related Practice
Textbook Question
(b) What is the change in potential energy if the distance separating the two electrons is increased to 1.0 nm?
Textbook Question
(c) Does the potential energy of the two particles increase or decrease when the distance is increased to 1.0 nm?
Textbook Question
(a) The electrostatic force (not energy) of attraction between two oppositely charged objects is given by the equation F = k (Q1Q2/d2) where k = 8.99⨉109N-m2/C2, Q1 and Q2 are the charges of the two objects in Coulombs, and d is the distance separating the two objects in meters. What is the electrostatic force of attraction (in Newtons) between an electron and a proton that are separated by 1⨉102 pm?
Textbook Question
A sodium ion, Na+, with a charge of 1.6⨉10-19 C and a chloride ion, Cl - , with charge of -1.6⨉10-19 C, are separated by a distance of 0.50 nm. How much work would be required to increase the separation of the two ions to an infinite distance?