Potassium-40 decays to argon-40 with a half-life of 1.27 * 109 yr. What is the age of a rock in which the mass ratio of 40Ar to 40K is 4.2?
Ch.21 - Nuclear Chemistry

Brown14th EditionChemistry: The Central ScienceISBN: 9780134414232Not the one you use?Change textbook
Chapter 21, Problem 45
An analytical laboratory balance typically measures mass to the nearest 0.1 mg. What energy change would accompany the loss of 0.1 mg in mass, according to Einstein's mass-energy equivalence principle (E=mc²)?
 Verified step by step guidance
Verified step by step guidance1
Step 1: Identify the given values. The mass loss \( \Delta m \) is 0.1 mg, which needs to be converted to kilograms for use in the equation. Remember that 1 mg = 1 \times 10^{-3} \) g and 1 g = 1 \times 10^{-3} \) kg.
Step 2: Convert the mass loss from milligrams to kilograms. Use the conversion factors to find \( \Delta m \) in kg.
Step 3: Recall Einstein's mass-energy equivalence principle, which is given by the equation \( E = mc^2 \), where \( E \) is the energy, \( m \) is the mass, and \( c \) is the speed of light in a vacuum (approximately \( 3 \times 10^8 \) m/s).
Step 4: Substitute the converted mass \( \Delta m \) and the speed of light \( c \) into the equation \( E = mc^2 \) to calculate the energy change \( E \).
Step 5: Perform the multiplication to find the energy change \( E \) in joules, keeping track of the units to ensure they are consistent.
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Mass-Energy Equivalence
Mass-energy equivalence is a principle formulated by Albert Einstein, expressed by the equation E=mc², which states that mass (m) can be converted into energy (E) and vice versa. In this equation, c represents the speed of light in a vacuum, a constant that indicates the immense amount of energy contained in even a small amount of mass. This principle is fundamental in understanding nuclear reactions and the energy produced in processes like fusion and fission.
Recommended video:
Guided course
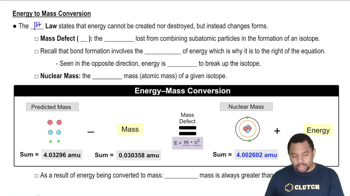
Energy to Mass Conversion
Analytical Balance
An analytical balance is a highly sensitive instrument used in laboratories to measure mass with great precision, often to the nearest 0.1 mg or better. It operates on the principle of electromagnetic force restoration, where the mass of the sample is balanced against a known force. The accuracy of these balances is crucial in quantitative analysis, as even minute differences in mass can significantly affect experimental results and calculations.
Recommended video:
Guided course

Balancing Chemical Equations
Energy Change Calculation
To calculate the energy change associated with a mass loss using the mass-energy equivalence principle, one can substitute the mass value into the equation E=mc². For a mass loss of 0.1 mg (or 0.0001 g), this involves converting grams to kilograms (0.0001 g = 1.0 x 10^-7 kg) and then multiplying by the square of the speed of light (approximately 3.00 x 10^8 m/s). This calculation reveals the energy released or absorbed due to the change in mass, illustrating the profound relationship between mass and energy.
Recommended video:
Guided course

Entropy in Phase Changes
Related Practice
Textbook Question
Textbook Question
The thermite reaction, Fe2O31s2 + 2 Al1s2 ¡2 Fe1s2 + Al2O31s2, H = -851.5 kJ>mol, is one of the most exothermic reactions known. Because the heat released is sufficient to melt the iron product, the reaction is used to weld metal under the ocean. How much heat is released per mole of Al2O3 produced? How does this amount of thermal energy compare with the energy released when 2 mol of protons and 2 mol of neutrons combine to form 1 mol of alpha particles?
Textbook Question
How much energy must be supplied to break a single aluminum-27 nucleus into separated protons and neutrons if an aluminum-27 atom has a mass of 26.9815386 amu? How much energy is required for 100.0 g of aluminum-27? (The mass of an electron is given on the inside back cover.)
