Textbook Question
During a period of discharge of a lead–acid battery, 402 g of Pb from the anode is converted into PbSO4(s). (b) How many coulombs of electrical charge are transferred from Pb to PbO2?
Ch.20 - Electrochemistry
Chapter 20, Problem 75
Heart pacemakers are often powered by lithium–silver chromate “button” batteries. The overall cell reaction is 2 Li(s) + Ag2CrO4(s) → Li2CrO4(s) + 2 Ag(s). Calculate the emf that would be generated at body temperature, 37 °C. How does this compare to the emf you calculated in part (b)?
Verified step by step guidance1
Identify the half-reactions involved in the cell reaction. The oxidation half-reaction is: 2 Li(s) → 2 Li⁺ + 2 e⁻. The reduction half-reaction is: Ag₂CrO₄(s) + 2 e⁻ → 2 Ag(s) + CrO₄²⁻.
Determine the standard reduction potentials for each half-reaction from a standard reduction potential table. The standard reduction potential for lithium is typically negative, indicating it is a strong reducing agent.
Calculate the standard cell potential (E°) using the formula: E° = E°(reduction) - E°(oxidation). Substitute the values obtained from the standard reduction potential table into this formula.
Adjust the standard cell potential to the body temperature of 37 °C using the Nernst equation: E = E° - (RT/nF) * ln(Q), where R is the gas constant, T is the temperature in Kelvin, n is the number of moles of electrons transferred, F is Faraday's constant, and Q is the reaction quotient.
Compare the calculated emf at 37 °C with the emf calculated in part (b) to understand how temperature affects the cell potential. Consider factors such as entropy and enthalpy changes that might influence the emf at different temperatures.
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Electrochemical Cells
Electrochemical cells convert chemical energy into electrical energy through redox reactions. In these cells, oxidation occurs at the anode and reduction at the cathode, generating a flow of electrons that can be harnessed as electric current. Understanding the components and functioning of electrochemical cells is crucial for calculating the electromotive force (emf) of the reaction.
Recommended video:
Guided course
02:46
Electrochemical Cells
Nernst Equation
The Nernst equation relates the emf of an electrochemical cell to the concentrations of the reactants and products, as well as the temperature. It is expressed as E = E° - (RT/nF)ln(Q), where E° is the standard emf, R is the gas constant, T is the temperature in Kelvin, n is the number of moles of electrons transferred, F is Faraday's constant, and Q is the reaction quotient. This equation is essential for calculating the emf at non-standard conditions, such as body temperature.
Recommended video:
Guided course
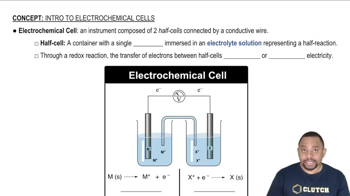
01:17The Nernst Equation
Standard Electrode Potentials
Standard electrode potentials are measured voltages for half-reactions under standard conditions (1 M concentration, 1 atm pressure, and 25 °C). These values are used to determine the overall cell potential by combining the reduction potential of the cathode and the oxidation potential of the anode. Knowing these potentials allows for the calculation of the standard emf, which can then be adjusted using the Nernst equation for different temperatures.
Recommended video:
Guided course
01:27Standard Cell Potential
Related Practice
Textbook Question
During the discharge of an alkaline battery, 4.50 g of Zn is consumed at the anode of the battery. (a) What mass of MnO2 is reduced at the cathode during this discharge?
Textbook Question
During the discharge of an alkaline battery, 4.50 g of Zn is consumed at the anode of the battery. (b) How many coulombs of electrical charge are transferred from Zn to MnO2?
Textbook Question
Heart pacemakers are often powered by lithium–silver chromate 'button' batteries. The overall cell reaction is 2 Li(s) + Ag2CrO4(s) → Li2CrO4(s) + 2 Ag(s) (a) Lithium metal is the reactant at one of the electrodes of the battery. Is it the anode or the cathode?
Textbook Question
Heart pacemakers are often powered by lithium–silver chromate 'button' batteries. The overall cell reaction is 2 Li(s) + Ag2CrO4(s) → Li2CrO4(s) + 2 Ag(s) (b) Choose the two half-reactions from Appendix E that most closely approximate the reactions that occur in the battery. What standard emf would be generated by a voltaic cell based on these half-reactions?