Textbook Question
A voltaic cell utilizes the following reaction: 4 Fe2+1aq2 + O21g2 + 4 H+1aq2 ¡ 4 Fe3+1aq2 + 2 H2O1l2 (a) What is the emf of this cell under standard conditions?
Ch.20 - Electrochemistry
Chapter 20, Problem 68b
A voltaic cell utilizes the following reaction: (b) What is the emf for this cell when 3Fe3+4 = 3.50 M, PH2= 0.95 atm, 3Fe2+4 = 0.0010 M, and the pH in both half-cells is 4.00?
Verified step by step guidance1
Identify the half-reactions and write the overall balanced equation for the cell. For a voltaic cell involving iron and hydrogen, the anode (oxidation) reaction might be Fe2+ -> Fe3+ + e-, and the cathode (reduction) reaction might be 2H+ + 2e- -> H2.
Use the Nernst equation to calculate the emf of the cell. The Nernst equation is E = E^0 - (RT/nF) * lnQ, where E^0 is the standard cell potential, R is the gas constant, T is the temperature in Kelvin, n is the number of moles of electrons transferred, F is the Faraday constant, and Q is the reaction quotient.
Calculate the reaction quotient, Q, for the cell reaction. Q is given by the expression Q = ([Fe3+]^3 * PH2) / ([Fe2+]^3 * [H+]^4). Use the given concentrations and pressures, and remember to convert pH to [H+] using [H+] = 10^(-pH).
Substitute the values of E^0, R, T, n, F, and Q into the Nernst equation. Use standard conditions and values for E^0, R, T, and F. For this reaction at 25°C (298 K), R = 8.314 J/(mol*K) and F = 96485 C/mol.
Solve the Nernst equation to find the emf, E, of the cell. This will give you the potential difference driving the cell under the specified non-standard conditions.
Verified video answer for a similar problem:
This video solution was recommended by our tutors as helpful for the problem above.
Video duration:
12mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Electrochemical Cells
Electrochemical cells, such as voltaic cells, convert chemical energy into electrical energy through redox reactions. In these cells, oxidation occurs at the anode and reduction at the cathode, allowing for the flow of electrons through an external circuit. Understanding the components and functioning of these cells is essential for calculating their electromotive force (emf).
Recommended video:
Guided course
02:46
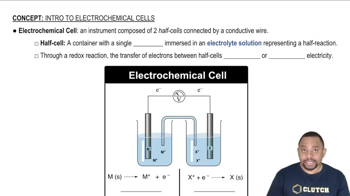
Electrochemical Cells
Nernst Equation
The Nernst equation relates the emf of an electrochemical cell to the concentrations of the reactants and products involved in the redox reaction. It accounts for non-standard conditions, allowing for the calculation of the cell potential based on the concentrations of ions and gases. This equation is crucial for determining the emf in the given scenario with varying concentrations and pressures.
Recommended video:
Guided course
01:17The Nernst Equation
pH and Its Effect on Cell Potential
pH is a measure of the hydrogen ion concentration in a solution, which can significantly influence the behavior of electrochemical reactions. In the context of a voltaic cell, changes in pH can affect the concentration of H+ ions, thereby impacting the equilibrium and the overall cell potential. Understanding how pH interacts with the redox reactions is vital for accurate emf calculations.
Recommended video:
Guided course
01:27Standard Cell Potential
Related Practice
Textbook Question
A voltaic cell utilizes the following reaction: 4 Fe2+1aq2 + O21g2 + 4 H+1aq2 ¡ 4 Fe3+1aq2 + 2 H2O1l2 (b) What is the emf of this cell when 3Fe2+4 = 1.3 M, 3Fe3+4= 0.010 M, PO2 = 0.50 atm, and the pH of the solution in the cathode half-cell is 3.50?
Textbook Question
A voltaic cell utilizes the following reaction: 2 Fe3+1aq2 + H21g2 ¡ 2 Fe2+1aq2 + 2 H+1aq2 (a) What is the emf of this cell under standard conditions?
Textbook Question
A voltaic cell is constructed that is based on the following reaction: Sn2+(aq) + Pb(s) → Sn(s) + Pb2+(aq) (a) If the concentration of Sn2+ in the cathode half-cell is 1.00 M and the cell generates an emf of +0.22 V, what is the concentration of Pb2+ in the anode half-cell?