Textbook Question
Calculate the pH of a solution made by adding 2.50 g of lithium oxide 1Li2O2 to enough water to make 1.500 L of solution.

 Verified step by step guidance
Verified step by step guidance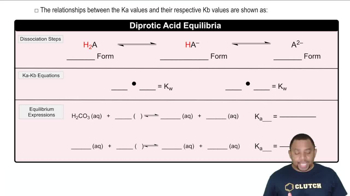


Calculate the pH of a solution made by adding 2.50 g of lithium oxide 1Li2O2 to enough water to make 1.500 L of solution.
Butyric acid is responsible for the foul smell of rancid butter. The pKa of butyric acid is 4.84. (a) Calculate the pKb for the butyrate ion.
Butyric acid is responsible for the foul smell of rancid butter. The pKa of butyric acid is 4.84. (b) Calculate the pH of a 0.050 M solution of butyric acid.
Butyric acid is responsible for the foul smell of rancid butter. The pKa of butyric acid is 4.84. (c) Calculate the pH of a 0.050 M solution of sodium butyrate.