Textbook Question
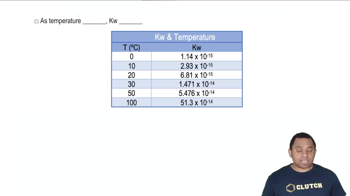
At 28 C, raw milk sours in 4.0 h but takes 48 h to sour in a refrigerator at 5 C. Estimate the activation energy in kJ>mol for the reaction that leads to the souring of milk.
Ch.14 - Chemical Kinetics
Chapter 14, Problem 106
The following is a quote from an article in the August 18, 1998, issue of The New York Times about the breakdown of cellulose and starch: “A drop of 18 degrees Fahrenheit [from 77 _x001E_F to 59 _x001E_F] lowers the reaction rate six times; a 36-degree drop [from 77 _x001E_F to 41 _x001E_F] produces a fortyfold decrease in the rate.” (b) Assuming the value of Ea calculated from the 36 _x001E_ drop and that the rate of breakdown is first order with a half-life at 25 _x001E_C of 2.7 yr, calculate the half-life for breakdown at a temperature of -15 _x001E_C.
Verified step by step guidance1
Step 1: Convert the given temperatures from Fahrenheit to Celsius. Use the formula: \( T(\degree C) = \frac{5}{9} (T(\degree F) - 32) \).
Step 2: Use the Arrhenius equation to relate the rate constants at different temperatures: \( k = A e^{-\frac{E_a}{RT}} \). Since the rate decreases by a factor of 40, set up the equation \( \frac{k_2}{k_1} = 40 \) and solve for \( E_a \) using the temperatures in Kelvin.
Step 3: Convert the temperatures from Celsius to Kelvin using \( T(K) = T(\degree C) + 273.15 \).
Step 4: Use the first-order kinetics formula for half-life: \( t_{1/2} = \frac{0.693}{k} \). Calculate the new rate constant \( k \) at -15 \degree C using the Arrhenius equation and the previously calculated \( E_a \).
Step 5: Calculate the half-life at -15 \degree C using the new rate constant \( k \) and the first-order half-life formula.
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Arrhenius Equation
The Arrhenius equation describes how the rate of a chemical reaction depends on temperature and activation energy (Ea). It states that the rate constant (k) increases exponentially with an increase in temperature, which can be expressed as k = A * e^(-Ea/RT), where A is the pre-exponential factor, R is the gas constant, and T is the temperature in Kelvin. Understanding this relationship is crucial for predicting how reaction rates change with temperature.
Recommended video:
Guided course
01:20
Arrhenius Equation
First-Order Reactions
First-order reactions are those where the rate of reaction is directly proportional to the concentration of one reactant. The half-life of a first-order reaction is constant and independent of the initial concentration, calculated using the formula t1/2 = 0.693/k. This concept is essential for determining how long it takes for half of the reactant to be consumed, especially when temperature changes affect the rate constant.
Recommended video:
Guided course
02:29First-Order Reactions
Temperature Dependence of Reaction Rates
The temperature dependence of reaction rates indicates that as temperature decreases, the kinetic energy of molecules also decreases, leading to fewer effective collisions and a slower reaction rate. This is quantitatively described by the Arrhenius equation, which shows that a significant drop in temperature can lead to a dramatic decrease in reaction rates, as illustrated by the quoted article's findings on cellulose and starch breakdown.
Recommended video:
Guided course
01:24Kw Temperature Dependence
Related Practice
Textbook Question
The following mechanism has been proposed for the reaction of NO with H2 to form N2O and H2O:
NO(g) + NO(g) → N2O2(g)
N2O2(g) + H2(g) → N2O(g) + H2O(g)
(a) Show that the elementary reactions of the proposed mechanism add to provide a balanced equation for the reaction.
Textbook Question
The following mechanism has been proposed for the reaction of NO with H2 to form N2O and H2O:
NO(g) + NO(g) → N2O2(g)
N2O2(g) + H2(g) → N2O(g) + H2O(g)
(d) The observed rate law is rate = k[NO]2[H2]. If the proposed mechanism is correct, what can we conclude about the relative speeds of the first and second reactions?
Textbook Question
Ozone in the upper atmosphere can be destroyed by the following two-step mechanism:
Cl(g) + O3(g) → ClO(g) + O2(g)
ClO(g) + O(g) → Cl(g) + O2(g)
(a) What is the overall equation for this process?