Based on the data given in Table 13.4, which solution would give the larger freezing-point lowering, a 0.030 m solution of NaCl or a 0.020 m solution of K2SO4?

Verified step by step guidance

Step 1: Understand the concept of freezing-point depression, which is a colligative property. It depends on the number of solute particles in a solution, not their identity.

Step 2: Use the formula for freezing-point depression: \( \Delta T_f = i \cdot K_f \cdot m \), where \( \Delta T_f \) is the freezing-point depression, \( i \) is the van't Hoff factor, \( K_f \) is the freezing-point depression constant, and \( m \) is the molality of the solution.

Step 3: Determine the van't Hoff factor \( i \) for each solute. For NaCl, which dissociates into Na\(^+\) and Cl\(^-\), \( i = 2 \). For K\(_2\)SO\(_4\), which dissociates into 2 K\(^+\) and SO\(_4\)\(^{2-}\), \( i = 3 \).

Step 4: Calculate the effective molality for each solution by multiplying the molality by the van't Hoff factor: \( 0.030 \text{ m} \times 2 \) for NaCl and \( 0.020 \text{ m} \times 3 \) for K\(_2\)SO\(_4\).

Step 5: Compare the effective molalities to determine which solution has a larger freezing-point lowering. The solution with the higher effective molality will have a greater freezing-point depression.

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Freezing Point Depression

Freezing point depression is a colligative property that describes how the freezing point of a solvent decreases when a solute is added. The extent of this depression depends on the number of solute particles in solution rather than their identity. The formula for calculating freezing point depression is ΔTf = i * Kf * m, where 'i' is the van 't Hoff factor, 'Kf' is the freezing point depression constant, and 'm' is the molality of the solution.

Van 't Hoff Factor (i)

The van 't Hoff factor (i) indicates the number of particles into which a solute dissociates in solution. For example, NaCl dissociates into two ions (Na+ and Cl-), so i = 2, while K2SO4 dissociates into three ions (2 K+ and SO4^2-), giving i = 3. This factor is crucial for calculating colligative properties, as it directly affects the total number of solute particles in the solution.

Molality (m)

Molality (m) is a measure of the concentration of a solute in a solution, defined as the number of moles of solute per kilogram of solvent. It is particularly useful in colligative property calculations because it remains unaffected by temperature changes, unlike molarity. In this question, the molalities of the NaCl and K2SO4 solutions are essential for determining their respective freezing point depressions.

Recommended video:

Guided course

00:40

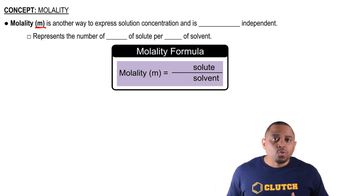
Molality

Related Practice

Textbook Question

Lysozyme is an enzyme that breaks bacterial cell walls. A solution containing 0.150 g of this enzyme in 210 mL of solution has an osmotic pressure of 0.953 torr at 25 °C. What is the molar mass of lysozyme?

Textbook Question

A dilute aqueous solution of an organic compound soluble in water is formed by dissolving 2.35 g of the compound in water to form 0.250 L of solution. The resulting solution has an osmotic pressure of 0.605 atm at 25 °C. Assuming that the organic compound is a nonelectrolyte, what is its molar mass?

Textbook Question

The osmotic pressure of a 0.010 M aqueous solution of CaCl₂ is found to be 0.674 atm at 25 °C. Calculate the van't Hoff factor, i, for the solution.

Textbook Question

Aerosols are important components of the atmosphere. Does the presence of aerosols in the atmosphere increase or decrease the amount of sunlight that arrives at the Earth's surface, compared to an 'aerosol-free' atmosphere? Explain your reasoning.