Acetonitrile (CH3CN) is a polar organic solvent that dissolves a wide range of solutes, including many salts. The density of a 1.80 M LiBr solution in acetonitrile is 0.826 g/cm3. Calculate the concentration of the solution in (a) molality,

A 'canned heat' product used to warm buffet dishes consists of a homogeneous mixture of ethanol 1C2H5OH2 andparaffin, which has an average formula of C24H50. Whatmass of C2H5OH should be added to 620 kg of the paraffinto produce 8 torr of ethanol vapor pressure at 35 °C? Thevapor pressure of pure ethanol at 35 °C is 100 torr.
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
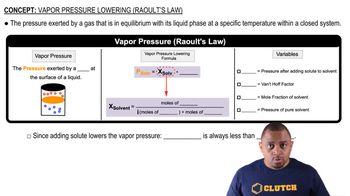
Raoult's Law
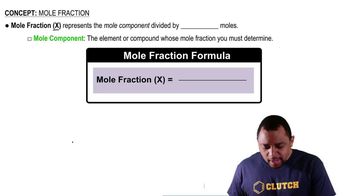
Mole Fraction
Vapor Pressure

Acetonitrile (CH3CN) is a polar organic solvent that dissolves a wide range of solutes, including many salts. The density of a 1.80 M LiBr solution in acetonitrile is 0.826 g/cm3. Calculate the concentration of the solution in (b) mole fraction of LiBr,
Acetonitrile (CH3CN) is a polar organic solvent that dissolves a wide range of solutes, including many salts. The density of a 1.80 M LiBr solution in acetonitrile is 0.826 g/cm3. Calculate the concentration of the solution in (c) mass percentage of CH3CN.
Two beakers are placed in a sealed box at 25 °C. One beaker contains 30.0 mL of a 0.050 M aqueous solution of a nonvolatile nonelectrolyte. The other beaker contains 30.0 mL of a 0.035 M aqueous solution of NaCl. The water vapor from the two solutions reaches equilibrium. (a) In which beaker does the solution level rise, and in which one does it fall?
Two beakers are placed in a sealed box at 25 °C. One beaker contains 30.0 mL of a 0.050 M aqueous solution of a nonvolatile nonelectrolyte. The other beaker contains 30.0 mL of a 0.035 M aqueous solution of NaCl. The water vapor from the two solutions reaches equilibrium. (b) What are the volumes in the two beakers when equilibrium is attained, assuming ideal behavior?
