Here are the essential concepts you must grasp in order to answer the question correctly.
Band Gap Energy
The band gap energy is the energy difference between the valence band and the conduction band in a solid material. It determines the electrical conductivity and optical properties of the material. In semiconductors and insulators, a larger band gap typically means that the material requires more energy to excite electrons from the valence band to the conduction band, influencing the wavelengths of light it can absorb or emit.
Recommended video:
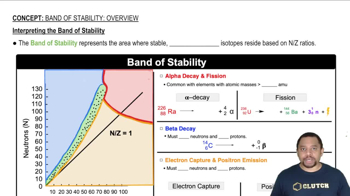
Intepreting the Band of Stability
Photon Energy and Wavelength Relationship
The energy of a photon is inversely related to its wavelength, described by the equation E = hc/λ, where E is energy, h is Planck's constant, c is the speed of light, and λ is the wavelength. This relationship indicates that higher energy photons correspond to shorter wavelengths, while lower energy photons correspond to longer wavelengths. Understanding this relationship is crucial for converting band gap energy into the corresponding wavelength of light.
Recommended video:
Frequency-Wavelength Relationship
Planck's Constant
Planck's constant (h) is a fundamental constant in quantum mechanics that relates the energy of a photon to its frequency. Its value is approximately 6.626 x 10^-34 J·s. This constant is essential for calculations involving photon energy and is used in the equation E = hf, where f is the frequency of the photon. It plays a critical role in determining the energy associated with electromagnetic radiation.
Recommended video:
Photons and Planck's Constant

 Verified step by step guidance
Verified step by step guidance