You are assigned the task of separating a desired granular material with a density of 3.62 g/cm3 from an undesired granular material that has a density of 2.04 g/cm3. You want to do this by shaking the mixture in a liquid in which the heavier material will fall to the bottom and the lighter material will float. A solid will float on any liquid that is more dense. Using an Internet-based source or a handbook of chemistry, find the densities of the following substances: carbon tetrachloride, hexane, benzene, and diiodomethane. Which of these liquids will serve your purpose, assuming no chemical interaction takes place between the liquid and the solids?
Ch.1 - Introduction: Matter, Energy, and Measurement

Brown14th EditionChemistry: The Central ScienceISBN: 9780134414232Not the one you use?Change textbook
Chapter 1, Problem 103
U.S. 1-cent coin (a penny) has a diameter of 19 mm and athickness of 1.5 mm. Assume the coin is made of pure copper,whose density and approximate market price are 8.9 g/cm3and \$2.40 per pound, respectively. Calculate the value ofthe copper in the coin, assuming its thickness is uniform.
 Verified step by step guidance
Verified step by step guidance1
Convert the dimensions of the penny from millimeters to centimeters: diameter = 1.9 cm and thickness = 0.15 cm.
Calculate the volume of the penny using the formula for the volume of a cylinder: \( V = \pi r^2 h \), where \( r \) is the radius and \( h \) is the height (thickness).
Determine the mass of the penny by multiplying the volume by the density of copper: \( \text{mass} = \text{volume} \times 8.9 \text{ g/cm}^3 \).
Convert the mass from grams to pounds, knowing that 1 pound is approximately 453.592 grams.
Calculate the value of the copper in the penny by multiplying the mass in pounds by the market price of copper, which is \$2.40 per pound.

Verified video answer for a similar problem:
This video solution was recommended by our tutors as helpful for the problem above.
Video duration:
4mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Density
Density is defined as mass per unit volume and is a crucial property of materials. In this context, the density of copper (8.9 g/cm³) allows us to calculate the mass of the penny once its volume is determined. Understanding how to convert between units of measurement, such as from mm³ to cm³, is essential for accurate calculations.
Recommended video:
Guided course

Density Concepts
Volume of a Cylinder
The penny can be approximated as a cylinder, and its volume can be calculated using the formula V = πr²h, where r is the radius and h is the height (or thickness). This geometric understanding is vital for determining how much copper is present in the coin, which directly influences its mass and value.
Recommended video:
Guided course
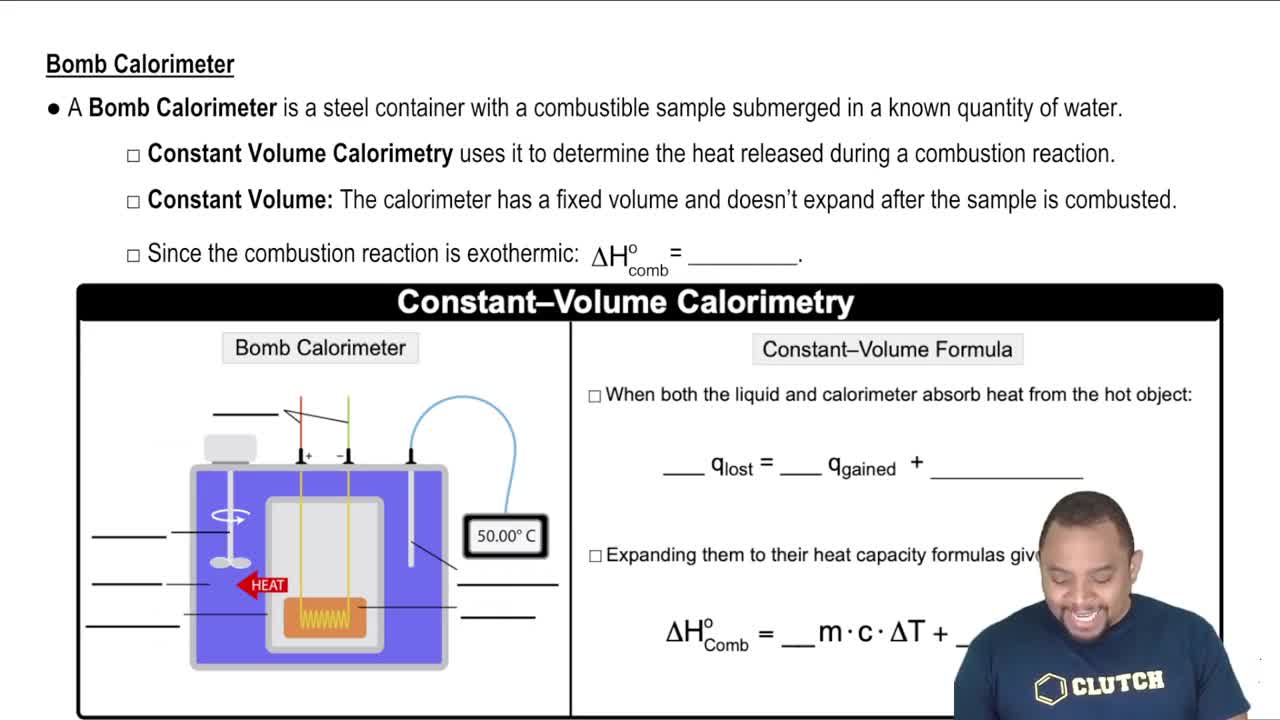
Constant-Volume Calorimetry
Conversion of Units
In this problem, converting units is necessary to find the value of copper in the penny. The mass of copper needs to be converted from grams to pounds to match the market price given in dollars per pound. Mastery of unit conversion ensures that calculations are consistent and accurate, allowing for the correct determination of the coin's value.
Recommended video:
Guided course

Conversion Factors
Related Practice
Textbook Question
Textbook Question
In 2009, a team from Northwestern University and Western Washington University reported the preparation of a new 'spongy' material composed of nickel, molybdenum, and sulfur that excels at removing mercury from water. The density of this new material is 0.20 g/cm3, and its surface area is 1242 m2 per gram of material. (b) Calculate the surface area for a 10.0-mg sample of this material.
2
views
Textbook Question
(c) Using the volume of a silver atom and the formula for the volume of a sphere, calculate the radius in angstroms of a silver atom.
