Open Question
Which property is used to determine if an object is made of pure silver (Ag)?
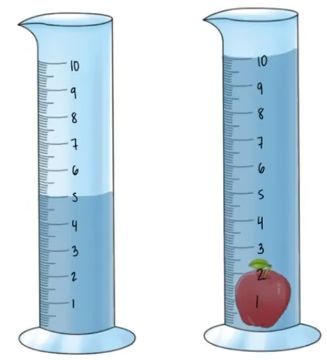
4000 mg
5000 mg
0.0048 mg
4800 mg
5300 mg
 Verified step by step guidance
Verified step by step guidance
 3:01m
3:01mMaster Density via Water Displacement with a bite sized video explanation from Jules
Start learning
