(b) List two reasons why the gases deviate from ideal behavior.

Based on their respective van der Waals constants( Table 10.3), is Ar or CO2 expected to behave more nearlylike an ideal gas at high pressures?
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
Ideal Gas Law

Van der Waals Equation

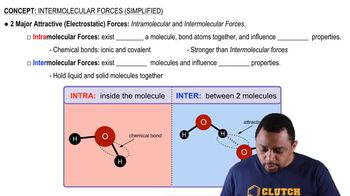
Intermolecular Forces
The planet Jupiter has a surface temperature of 140 K and a mass 318 times that of Earth. Mercury (the planet) has a surface temperature between 600 K and 700 K and a mass 0.05 times that of Earth. On which planet is the atmosphere more likely to obey the ideal-gas law? Explain.
Which statement concerning the van der Waals constants a and b is true? (a) The magnitude of a relates to molecular volume, whereas b relates to attractions between molecules. (b) The magnitude of a relates to attractions between molecules, whereas b relates to molecular volume. (c) The magnitudes of a and b depend on pressure. (d) The magnitudes of a and b depend on temperature.
Calculate the pressure that CCl4 will exert at 80 °C if 1.00 mol occupies 33.3 L, assuming that (a) CCl4 obeys the ideal-gas equation (b) CCl4 obeys the van der Waals equation. (Values for the van der Waals constants are given in Table 10.3.)
Calculate the pressure that CCl4 will exert at 80 °C if 1.00 mol occupies 33.3 L, assuming that (c) Which would you expect to deviate more from ideal behavior under these conditions, Cl2 or CCl4? Explain.
