Arsenic(III) sulfide sublimes readily, even below its melting point of 320 °C. The molecules of the vapor phase are found to effuse through a tiny hole at 0.52 times the rate of effusion of Xe atoms under the same conditions of temperature and pressure. What is the molecular formula of arsenic(III) sulfide in the gas phase?

(b) List two reasons why the gases deviate from ideal behavior.
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
Ideal Gas Law

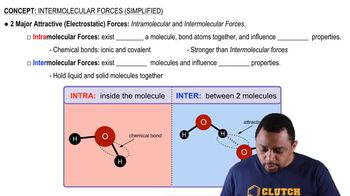
Intermolecular Forces
Molecular Volume
A gas of unknown molecular mass was allowed to effuse through a small opening under constant-pressure conditions. It required 105 s for 1.0 L of the gas to effuse. Under identical experimental conditions it required 31 s for 1.0 L of O2 gas to effuse. Calculate the molar mass of the unknown gas. (Remember that the faster the rate of effusion, the shorter the time required for effusion of 1.0 L; in other words, rate is the amount that diffuses over the time it takes to diffuse.)
The planet Jupiter has a surface temperature of 140 K and a mass 318 times that of Earth. Mercury (the planet) has a surface temperature between 600 K and 700 K and a mass 0.05 times that of Earth. On which planet is the atmosphere more likely to obey the ideal-gas law? Explain.
Which statement concerning the van der Waals constants a and b is true? (a) The magnitude of a relates to molecular volume, whereas b relates to attractions between molecules. (b) The magnitude of a relates to attractions between molecules, whereas b relates to molecular volume. (c) The magnitudes of a and b depend on pressure. (d) The magnitudes of a and b depend on temperature.
