Textbook Question
A battery relies on the oxidation of magnesium and the reduction of Cu2+. The initial concentrations of Mg2+ and Cu2+ are 1.0 × 10–4 M and 1.5 M, respectively, in 1.0-liter half-cells. a. What is the initial voltage of the battery?
Ch.19 - Electrochemistry
Chapter 19, Problem 116a
A rechargeable battery is constructed based on a concentration cell constructed of two Ag/Ag+ half-cells. The volume of each half-cell is 2.0 L, and the concentrations of Ag+ in the half-cells are 1.25 M and 1.0×10–3 M. a. How long can this battery deliver 2.5 Aof current before it goes dead?
Verified step by step guidance1
Identify the half-reactions for the concentration cell. In a concentration cell, the same species is involved in both half-reactions, but at different concentrations. Here, the half-reaction is Ag+ + e- → Ag for both electrodes.
Calculate the cell potential (Ecell) using the Nernst equation: Ecell = E°cell - (RT/nF) * ln(Q), where E°cell is 0 for a concentration cell, R is the gas constant (8.314 J/mol·K), T is the temperature in Kelvin, n is the number of moles of electrons transferred (1 for Ag/Ag+), F is Faraday's constant (96485 C/mol), and Q is the reaction quotient, which is the ratio of the concentrations of Ag+ in the two half-cells.
Substitute the given concentrations into the Nernst equation. The reaction quotient Q is [Ag+]anode/[Ag+]cathode = 1.0×10^-3 M / 1.25 M.
Determine the total charge (Q) that can be delivered by the battery using the formula Q = n * F, where n is the number of moles of electrons transferred. Since the current (I) is given as 2.5 A, use the relationship Q = I * t to find the time (t) the battery can deliver this current.
Solve for time (t) using the equation t = Q/I, where Q is the total charge calculated in the previous step and I is the current (2.5 A). This will give you the duration for which the battery can deliver the specified current before it goes dead.
Verified video answer for a similar problem:
This video solution was recommended by our tutors as helpful for the problem above.
Video duration:
4mWas this helpful?
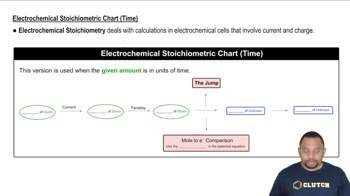
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Concentration Cells
A concentration cell is a type of electrochemical cell where the electrodes are the same material but are immersed in solutions of different concentrations. The potential difference arises from the difference in concentration of ions, driving the flow of electrons from the higher concentration to the lower concentration. This principle is crucial for understanding how the battery operates and generates electrical energy.
Recommended video:
Guided course
01:21
The Electrolytic Cell
Nernst Equation
The Nernst equation relates the cell potential to the concentrations of the reactants and products in an electrochemical reaction. It allows for the calculation of the electromotive force (EMF) of the cell based on the concentration of ions. This equation is essential for determining how the varying concentrations of Ag<sup>+</sup> in the half-cells affect the overall voltage and performance of the battery.
Recommended video:
Guided course
01:17The Nernst Equation
Current and Time Relationship
The relationship between current, charge, and time is described by the equation Q = I × t, where Q is the total charge, I is the current, and t is the time. This concept is vital for calculating how long the battery can deliver a specific current before depleting its charge. Understanding this relationship helps in determining the operational duration of the battery based on its capacity and the current draw.
Recommended video:
Guided course
02:16Electrochemical Stoichiometric Chart (Time)
Related Practice
Textbook Question
A battery relies on the oxidation of magnesium and the reduction of Cu2+. The initial concentrations of Mg2+ and Cu2+ are 1.0 × 10–4 M and 1.5 M, respectively, in 1.0-liter half-cells. b. What is the voltage of the battery after delivering 5.0 A for 8.0 h?
Textbook Question
A battery relies on the oxidation of magnesium and the reduction of Cu2+. The initial concentrations of Mg2+ and Cu2+ are 1.0 × 10–4 M and 1.5 M, respectively, in 1.0-liter half-cells. c. How long can the battery deliver 5.0 A before going dead?
Textbook Question
A rechargeable battery is constructed based on a concentration cell constructed of two Ag/Ag+ half-cells. The volume of each half-cell is 2.0 L, and the concentrations of Ag+ in the half-cells are 1.25 M and 1.0 × 10–3 M. b. What mass of silver is plated onto the cathode by running at 3.5 A for 5.5 h?
Textbook Question
A rechargeable battery is constructed based on a concentration cell constructed of two Ag/Ag+ half-cells. The volume of each half-cell is 2.0 L, and the concentrations of Ag+ in the half-cells are 1.25 M and 1.0 × 10–3 M. c. Upon recharging, how long would it take to redissolve 1.00 × 102 g of silver at a charging current of 10.0 amps?